[C#][VB] 優先度付きキューを実装する方法 │ Web備忘録

1. 優先度付きキュー(PriorityQueue)
2. 優先度付きキューと二分ヒープ
- 2.1. up-heap
  - 2.1.1. 実装
- 2.2. down-heap
  - 2.2.1. 実装
3. 優先度付きキュー(Priority Queue)の実装 (C#)
4. 使い方と動作確認
5. 優先度付きキュー(Priority Queue)の実装 (VB.NET)
6. 参考URL

優先度付きキュー(PriorityQueue)

優先度付きキュー(Priority Queue)は、優先度に従って優先的に要素を取り出せるコレクションです。

単純なキューだと先入れ先出し(FIFO)ですが、取り出すときに優先度の高い要素(例えば値の大きいもの)から順番に取り出せるというキューになります。例えば普通のキューだと 3, 5, 1 の順に入れるとその順番に取り出せますが、これを優先度に従って 5, 3, 1 の順番に取り出せるようになるのが優先度付きキューです。

優先度付きキューは要素の追加、取り出しが計算量 O(log n) 最大値の参照が O(1) で実現できます。配列のようなデータ構造だと最大値の取り出しに O(n) かかるので、その点では有利に働くデータ構造といえます。

.NET(C#, VB) には優先度付きキューのクラスは用意されていません。そのため必要ならば自前で実装する必要があります。

優先度付きキューと二分ヒープ

優先度付きキューは内部データの構造として配列を 二分ヒープ として使います。

二分ヒープ – Wikipedia

二分ヒープの説明は以下の通りです。

二分ヒープ（にぶんヒープ,バイナリヒープ,Binary heap）とは、二分木を使って作られるヒープ(データ構造)の特に単純な種類のひとつである。それは、二分木に、以下の2つの制約を追加したものとみなせる。

要素間の順序関係に従った比較によって、各々のノードはそのノードの子よりも大きいか等しくなるように配置される（heap property）

木は完全にバランスの取れた二分木（すべての葉は同じ高さにある）になるか、木のもっとも高い方がすべて埋まっていないならば、ノードは左から右へ順に埋まっていく（shape property）

例えば次のようなツリー構造が二分ヒープです。

    11
  5    8
3   4 7

ツリー構造のルートが優先度最大のデータになります。子ノードは親の要素より値が小さいものになります。

このように値の大きいものをルートにして、木構造でデータを管理するの二分ヒープです。

ちなみに上のようなツリー構造を配列で表現すると次のようになります。

[11, 5, 8, 3, 4, 7]

あるノードのインデックスを n とすると、左の子ノードは 2n + 1, 右の子ノードは 2n + 2 であらわされます。親のインデックスは (n - 1) / 2 です。

優先度付きキューを実装する際、内部データを二分ヒープで管理すると、常に優先度の高いデータを参照することが可能になります。

up-heap

二分ヒープの構造がわかったところで、このデータ構造からデータを出し入れする方法を考えます。まずはデータを追加する方法です。

二分ヒープにデータを追加します。データの追加は配列の末尾に行います。二分ヒープだと X の位置になります。

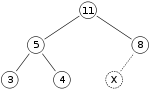
ここに「15」を追加します。ただし X の親が「8」なのでここに 15 はおけません。したがって 15 と 8 を入れ替えます。

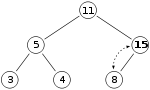
この状態でもまだ親のほうが値が小さいのでさらに親と入れ替えます。

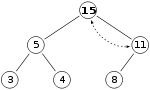
これで適切な二分ヒープになりました。このデータを追加した後に、末尾のデータが正しい位置に収まるまで親要素と交換し続ける処理を up-heap といいます。

up-heap の手順をまとめると次のようになります。

ヒープの最下層(配列の場合はヒープデータの直後)へデータを追加。
追加されたデータの親データと比較し、順序が正しければ処理完了。
比較結果が正しくなければ、親データと交換して、停止するまで2.を繰り返します。

実装

class PriorityQueue<T> where T : IComparable<T>
{
    public readonly T[] Array;
    public int Count { get; private set; } = 0;
    // ..

    private void UpHeap()
    {
        var n = this.Count - 1;
        while (n != 0)
        {
            // 親要素のインデックス
            var parent = (n - 1) / 2;
            if (this.Array[n].CompareTo(this.Array[parent]) > 0)
            {
                this.Swap(n, parent);
                n = parent;
            }
            else
            {
                break;
            }
        }
    }
}

こんな感じの実装になります。Swap() は要素を交換しているだけです。

nが二分ヒープの末尾の要素です。n番目の要素を親と比較して交換しています。これを停止できるまで続けます。

こうすることで配列の先頭が常に優先度の高いデータとなります。最終的な実装は後で紹介します。

down-heap

down-heap は二分ヒープからデータを取り出した後に、整合性を保つために必要となる処理です。

つまり up-heap が追加時の処理で down-heap が取り出し時の処理です。

up-heap と同じデータを例にデータの取り出しを考えます。

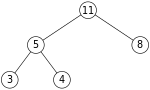
まず最大値、つまりルートの要素「11」を取り出します。

次に、末尾の要素を先頭にします。

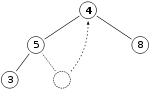
この状態から、先頭にした要素を子要素と交換しながら適切な位置まで移動させます。

親の「4」と子の「8」を比較して親のほうが小さいので交換します。※より大きいほうの子供と交換します。

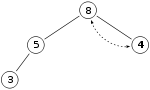
この状態で二分ヒープの整合性が保たれているので、処理終了です。必要があればさらに子の要素と比較を繰り返します。

down-heap の処理をまとめると以下のようになります。

ルートデータを取り出し、ヒープ最下層のデータと交換。
ルートデータを子データと比較し、正しい順序であれば処理完了。
比較結果が正しくなければ、子データと交換して、停止するまで2.を繰り返す。

実装

class PriorityQueue<T> where T : IComparable<T>
{
    public readonly T[] Array;
    public int Count { get; private set; } = 0;
    // ..

    private void DownHeap()
    {
        var parent = 0;
        while (true)
        {
            var child = 2 * parent + 1;
            if (child > this.Count - 1) break;

            if (child < this.Count - 1 && this.Array[child].CompareTo(this.Array[child + 1]) < 0)
            {
                // 左より右の子のほうが大きい値の場合、右を入れ替え対象にする
                child += 1;
            }

            if (this.Array[parent].CompareTo(this.Array[child]) < 0)
            {
                this.Swap(parent, child);
                parent = child;
            }
            else
            {
                break;
            }
        }
    }
}

先頭の要素を正当な位置まで繰り下げる処理です。

優先度付きキュー(Priority Queue)の実装 (C#)

UpHeap, DownHeap の処理を使って優先度付きキューを実装します。内部のデータは配列を使います。

それから最大値を取り出せる場合と最小値を取り出せる場合、両対応できるようにします。単純に比較時の判定を逆転させるだけで実現できます。

ということで実装全体が以下のようになります。

class PriorityQueue<T> where T : IComparable<T>
{
    public readonly T[] Array;
    public readonly bool Greater;
    public int Count { get; private set; } = 0;

    public PriorityQueue(int capacity, bool greater = true)
    {
        this.Array = new T[capacity];
        this.Greater = greater;
    }

    public void Enqueue(T item)
    {
        this.Array[this.Count] = item;
        this.Count += 1;
        this.UpHeap();
    }

    public T Dequeue()
    {
        // 先頭要素を末尾にして再構成
        this.Swap(0, this.Count - 1);
        this.Count -= 1;
        this.DownHeap();

        return this.Array[this.Count];
    }


    private void UpHeap()
    {
        var n = this.Count - 1;
        while (n != 0)
        {
            // 親要素の座標
            var parent = (n - 1) / 2;

            if (this.Compare(this.Array[n], this.Array[parent]) > 0)
            {
                this.Swap(n, parent);
                n = parent;
            }
            else
            {
                break;
            }
        }
    }

    private void DownHeap()
    {
        var parent = 0;
        while (true)
        {
            var child = 2 * parent + 1;
            if (child > this.Count - 1) break;

            if (child < this.Count - 1 && this.Compare(this.Array[child], this.Array[child + 1]) < 0)
            {
                // 左より右の子のほうが大きい値の場合、右を入れ替え対象にする
                child += 1;
            }

            if (this.Compare(this.Array[parent], this.Array[child]) < 0)
            {
                this.Swap(parent, child);
                parent = child;
            }
            else
            {
                break;
            }
        }
    }

    private int Compare(T a, T b)
    {
        var c = a.CompareTo(b);
        if (!this.Greater)
        {
            c = -c;
        }
        return c;
    }

    private void Swap(int a, int b)
    {
        var tmp = this.Array[a];
        this.Array[a] = this.Array[b];
        this.Array[b] = tmp;
    }
}

Enqueue(T item)

public void Enqueue(T item)
{
    this.Array[this.Count] = item;
    this.Count += 1;
    this.UpHeap();
}

まず二分ヒープの範囲末尾にデータを追加します。追加後カウントアップして、UpHeap を実行します。こうすることで末尾に追加した要素が、正しい位置まで繰り上がります。

この処理の後、先頭に最大値のデータが移動します。

Dequeu()

public T Dequeue()
{
    this.Swap(0, this.Count - 1);
    this.Count -= 1;
    this.DownHeap();

    return this.Array[this.Count];
}

まず配列の先頭要素が最大値のデータなので、これを末尾の要素と交換します。そしてカウントを減らして二分ヒープの範囲を制限し、先頭要素を DownHeap で繰り下げてだたしい位置に移動させます。

この処理の後、先頭に最大値のデータが移動します。

Compare()

private int Compare(T a, T b)
{
    var c = a.CompareTo(b);
    if (!this.Greater)
    {
        c = -c;
    }
    return c;
}

比較用の関数を用意します。

Greater が true の時、二分ヒープは最大値を取り出せるようになります。false の時、比較結果を反転するようにします。CompareTo() は比較結果の大小を 1, 0, -1 で返します。

よって比較結果を反転することで最大値最小値を切り替えられるようになります。

使い方と動作確認

内部のデータを配列で持つので最初にキャパシティを設定します。
Enqueue でデータを追加します。
Dequeue でデータ(最大値)を取り出します。

var q = new PriorityQueue<int>(5);

q.Enqueue(11);
q.Enqueue(3);
q.Enqueue(4);
q.Enqueue(8);
q.Enqueue(5);

var count = q.Count;
for (int i = 0; i < count; i++)
{
    // 11, 8, 5, 4, 3
    Console.WriteLine(q.Dequeue());
}

追加順にかかわらず最大値から取り出せているのがわかります。

優先度付きキュー(Priority Queue)の実装 (VB.NET)

Public Class PriorityQueue(Of T As IComparable)
    Public ReadOnly Property Array As T()
    Public ReadOnly Property greater As Boolean
    Public Property Count As Integer = 0

    Public Sub New(capacity As Integer, Optional greater As Boolean = True)
        Me.greater = greater
        ReDim Me.Array(capacity - 1)
    End Sub

    Public Sub Enqueue(item As T)
        Me.Array(Me.Count) = item
        Me.Count += 1
        Me.UpHeap()
    End Sub

    Public Function Dequeue() As T
        Me.Swap(0, Me.Count - 1)
        Me.Count -= 1
        Me.DownHeap()

        Return Me.Array(Me.Count)
    End Function

    Private Sub UpHeap()
        Dim n As Integer = Me.Count - 1
        While n <> 0
            Dim parent As Integer = (n - 1) / 2

            If Me.Compare(Me.Array(n), Me.Array(parent)) > 0 Then
                Me.Swap(n, parent)
                n = parent
            Else
                Exit While
            End If
        End While
    End Sub

    Private Sub DownHeap()
        Dim parent As Integer = 0
        While True
            Dim child As Integer = 2 * parent + 1
            If child > Me.Count - 1 Then
                Exit While
            End If

            If child < Me.Count - 1 AndAlso Me.Compare(Me.Array(child), Me.Array(child + 1)) < 0 Then
                child += 1
            End If

            If Me.Compare(Me.Array(parent), Me.Array(child)) < 0 Then
                Me.Swap(parent, child)
                parent = child
            Else
                Exit While
            End If
        End While
    End Sub

    Private Function Compare(a As T, b As T)
        Dim c As Integer = a.CompareTo(b)
        If Not Me.greater Then
            c = -c
        End If
        Return c
    End Function

    Private Sub Swap(a As Integer, b As Integer)
        Dim tmp = Me.Array(a)
        Me.Array(a) = Me.Array(b)
        Me.Array(b) = tmp
    End Sub
End Class

動かしてみるとこんな感じです。

Dim q = New PriorityQueue(Of Integer)(5)
q.Enqueue(11)
q.Enqueue(3)
q.Enqueue(4)
q.Enqueue(8)
q.Enqueue(5)

Dim count As Integer = q.Count
For index = 0 To count - 1
    ' 11, 8, 5, 4, 3
    Console.WriteLine(q.Dequeue())
Next

以上。

参考URL

[C#] Iterator パターン – デザインパターン入門

[C#][VB] 二分探索(バイナリサーチ)の実装

[C#][VB] 優先度付きキューを実装する方法

優先度付きキュー(PriorityQueue)

優先度付きキューと二分ヒープ

up-heap

実装

down-heap

実装

優先度付きキュー(Priority Queue)の実装 (C#)

Enqueue(T item)

Dequeu()

Compare()

使い方と動作確認

優先度付きキュー(Priority Queue)の実装 (VB.NET)

参考URL

アルゴリズムカテゴリの最新記事

SparseTable の実装と解説 [C#]

Suffix Array の解説と実装方法[C#][C++]

[C#] ベルマンフォード法で単一始点最短経路問題を解くための実装方法

[C#] 最小公倍数(LCM)を求めるアルゴリズムと実装

[C#] ユークリッドの互除法で最大公約数を求める方法

[C#] Union-Find木を実装する方法