[C#] Union-Find木を実装する方法

Union-Find木 とは

素集合データ構造は、データの集合を素集合（互いにオーバーラップしない集合）に分割して保持するデータ構造。このデータ構造に対する以下の2つの便利な操作をUnion-Findアルゴリズムと呼ぶ。

• Find: 特定の要素がどの集合に属しているかを求める。2つの要素が同じ集合に属しているかの判定にも使われる。
• Union: 2つの集合を1つに統合する。

これら2つの操作をサポートしているため、素集合データ構造は「Union-Findデータ構造」あるいは「Merge-Find集合」とも呼ばれる。

素集合データ構造 – Wikipedia

上記の通り、素集合データ構造のことを Union-Find木 といいます。2つのグループを同じグループにまとめる(Union)と、2つの要素が同じグループに属しているかの判定(Find)ができるデータ構造です。

例えば「友達の友達は友達である」というときに、「AとBは友達、BとCは友達」だとして、「AとCは友達だ」といった判定ができるようになります。

Union-Find木でできること

Union

Union は2つのグループを同じにまとめることができます。複数の要素からなるデータであり、初期状態ではそれぞれの要素が単独の要素からなるグループです。

ここで、1 と 2 が同じグループだとなったときに同じグループにくっつけることができます。

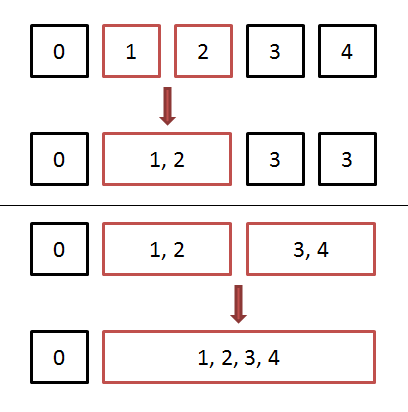
もちろん単一の要素同士でなくても、グループ同士を結合できます。

実装方法

データをグループにまとめるには、データごとにグループのラベルを割り振る方法が考えられます。ルートとなる親要素を決めその要素のインデックスをラベルとして保持するといい感じにまとめられます。

ただし愚直に実装を行うと、グループをまとめるときに全ての親をループして書き換えていくということをやることになって時間が O(n) かかってしまいます。

Union-Find木 ではデータを木構造で表現します。代表して1つの要素をルートと決めておき、まとめるときはルートだけを書き換えるようにします。こうすると高速でグループをまとめることができるようになります。

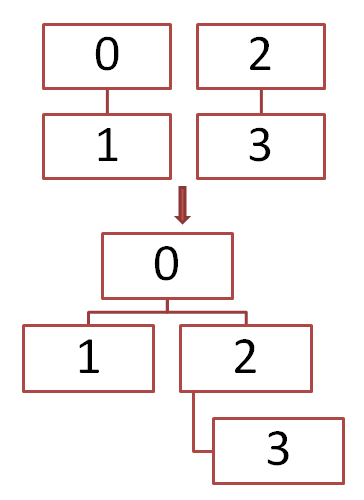
例えば上のように、2つのグループがあってこれらをまとめるとき、1のグループに3のグループをまとめると考え、3のルートを1につなぎかえます。

ただし例を見てもわかる通り、木構造に偏りが生じるのでこのままでもやはり効率が悪いです。よって、親をたどるタイミングですべてのグループ内の要素をルートにつなぎかえるという処理を行っていきます。詳しくは実装を確認してください。

実装は親のインデックスを配列でそれぞれに保持するようにして、これを書き換えるように作ります。

Find

Find は2つの要素が同じグループに属しているかの判定に使います。

要素ごとのルートが一致するかどうかで、同一グループかどうかを判定できます。

実装

では実装してみます。

上記機能のほかに、グループの要素数がわかるようにするために少し工夫します。

class UnionFind
{
    // 親要素のインデックスを保持する
    // 親要素が存在しない(自身がルートである)とき、マイナスでグループの要素数を持つ
    public int[] Parents { get; set; }
    public UnionFind(int n)
    {
        this.Parents = new int[n];
        for (int i = 0; i < n; i++)
        {
            // 初期状態ではそれぞれが別のグループ(ルートは自分自身)
            // ルートなのでマイナスで要素数(1個)を保持する
            this.Parents[i] = -1;
        }
    }

    // 要素xのルート要素はどれか
    public int Find(int x)
    {
        // 親がマイナスの場合は自分自身がルート
        if (this.Parents[x] < 0) return x;
        // ルートが見つかるまで再帰的に探す
        // 見つかったルートにつなぎかえる
        this.Parents[x] = Find(this.Parents[x]);
        return this.Parents[x];
    }

    // 要素xの属するグループの要素数を取得する
    public int Size(int x)
    {
        // ルート要素を取得して、サイズを取得して返す
        return -this.Parents[this.Find(x)];
    }

    // 要素x, yが同じグループかどうか判定する
    public bool Same(int x, int y)
    {
        return this.Find(x) == this.Find(y);
    }

    // 要素x, yが属するグループを同じグループにまとめる
    public bool Union(int x, int y)
    {
        // x, y のルート
        x = this.Find(x);
        y = this.Find(y);
        // すでに同じグループの場合処理しない
        if (x == y) return false;

        // 要素数が少ないグループを多いほうに書き換えたい
        if (this.Size(x) < this.Size(y))
        {
            var tmp = x;
            x = y;
            y = tmp;
        }
        // まとめる先のグループの要素数を更新
        this.Parents[x] += this.Parents[y];
        // まとめられるグループのルートの親を書き換え
        this.Parents[y] = x;
        return true;
    }
}

詳しくはコメントに書いた通りです。

Parents で要素の親を保持します。ただしルート要素の場合、マイナスの数でグループの要素数を保持するようにしてます。

Union find(素集合データ構造)

コードは上記ページのスライドを参考にして実装しました。

D – Decayed Bridges

上の問題で使ってACでたのでおそらく正しく実装されているのでしょう。

以上。