[C#] ユークリッドの互除法で最大公約数を求める方法

最大公約数を求めるプログラム

2つの自然数の最大公約数を求めるアルゴリズムの1つに、ユーグリッドの互除法 があります。これをプログラムで実装する方法をまとめます。

ユークリッドの互除法とは

ユークリッドの互除法 – Wikipedia

2 つの自然数 a, b (a ≧ b) について、a の b による剰余を r とすると、 a と b との最大公約数は b と r との最大公約数に等しいという性質が成り立つ。この性質を利用して、 b を r で割った剰余、 除数 r をその剰余で割った剰余、と剰余を求める計算を逐次繰り返すと、剰余が 0 になった時の除数が a と b との最大公約数となる。

手続き

2つの自然数 m, n についてユーグリッドの互除法で最大公約数を求めるアルゴリズムの手続きは以下のようになります。

1. 入力を m, n (m ≧ n) とする。
2. n = 0 なら、 m を出力してアルゴリズムを終了する。
3. m を n で割った余りを新たに n とし、更に 元のnを新たにm とし 2. に戻る。

この各手順について、図を使って具体例で見ていきます。

例

まず2つの自然数 m, n(m>=n) を目盛付きの棒で表します。1目盛が最大公約数と考えます。

図で表すとこんな感じです。

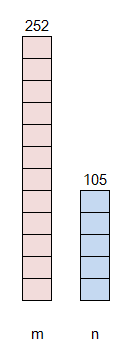
m=252, n=105 で考えます。

最大公約数は最小の場合で1、最大の場合でnになります。m, n いずれも 最大公約数*X みたいな形で表せるので、それを目盛で表現しています。

252 と 105 の最大公約数は 21 なので1目盛が21と思ってください。

これを上記手続きを使って処理を進めていくと次のようになります。

1. 252 を 105 で割った余りは 42
2. 105 を 42 で割った余りは 21
3. 42 を 21 で割った余りは 0
4. 21, 0 で手続きが呼び出され、0があるので 21 が最大公約数と決まる。

図にするとこんな感じです。

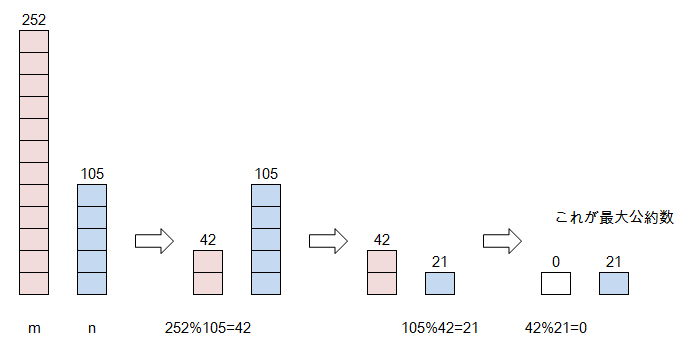
% はあまりを求める演算子です。

交互に余りをとっていき、最終的に余りが0になったときに答えが求まります。

なぜ答えがこれで求まるかは、この図を使った整理の仕方が個人的にはわかりやすかったです。

Wikipedia のアニメーションGIFも引用しておきます。

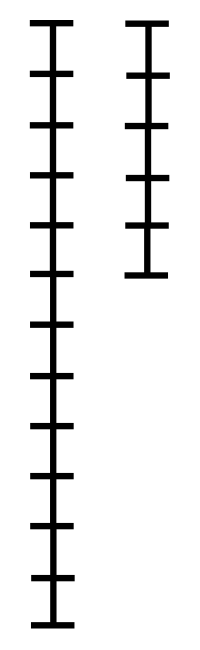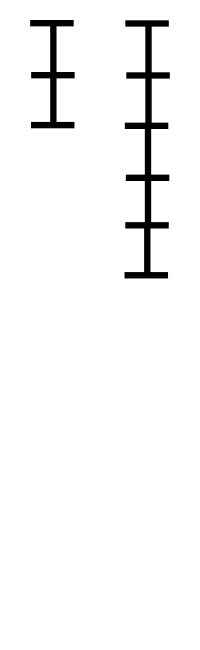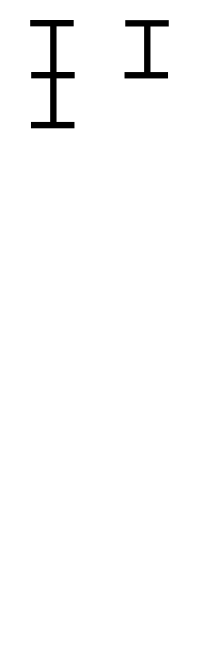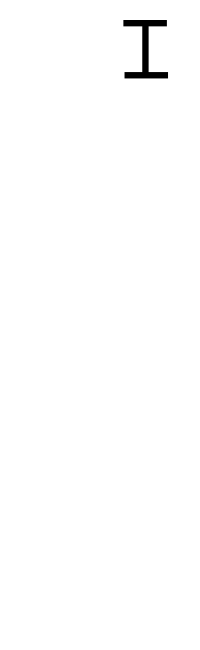
計算量

計算量は小さい方の自然数をnとすると O(log n) 回程度の呼び出しで答えが求まるようです。

ユークリッドの互除法 – Wikipedia

割って余りを取るという操作を、最悪でも小さい方の十進法での桁数の約 5 倍繰り返せば、最大公約数に達する（ラメの定理）。

…

入力された2つの整数のうち小さいほうの整数 n の桁数を d とすれば、ユークリッドの互除法では O(d) 回の除算で最大公約数が求められる。桁数 d は O(log n) なので、ユークリッドの互除法では O(log n) 回の除算で最大公約数が求められる。

実装 C#

ユークリッドの互除法のアルゴリズムが理解できたところで実装していきます。

その手続きからわかる通り、ユークリッドの互除法は再帰的に処理を繰り返すことになります。よって再帰関数を使うか、答えが求まるまでループして処理を続けるかのいずれかになります。

再帰関数の方がわかりやすいのでその方針で実装してみます。

使用する言語はC#です。C# には最大公約数や最小公倍数が標準ライブラリで提供されていないので、ほしければ自分で実装する必要があります。

static long Gcd(long m, long n)
{
    if (n == 0) return m;
    return Gcd(n, m % n);
}

非常にシンプルなコードになります。入力として2つの自然数を受け取っています。

m, n の大小関係は問いません。なぜなら n>m だとしても m%n = m になるので、次の呼び出しで2つの変数が入れ替わって呼び出されるからです。

あとは n=0 の時を終了条件として、その時の m を答えとして返します。

Console.WriteLine(Gcd(252, 105)); // 21
Console.WriteLine(Gcd(105, 252)); // 21
Console.WriteLine(Gcd(12, 4));    // 4
Console.WriteLine(Gcd(19, 5));    // 1

こんな感じで使えます。答えも正しく求まりました。

以上。