SparseTable の実装と解説 [C#] │ Web備忘録

1. Sparse Table とは
2. Sparse Table の仕組み
3. 実装(C#)
4. コード解説
5. 動作確認
6. 参考URL

Sparse Table とは

Sparse Table とは、静的なデータに対して、範囲最小クエリ(RMQ)に答えることができるデータ構造です。

RMQ に答えることができるデータ構造に Segment Tree がありますが、データの変更に対応できるかどうかという点で異なります。Sparse Table はデータの変更はできない代わりに、前計算を行った上でRMQに O(1) で答えることが可能になり、この点では Segment Tree に勝ります。

	Sparse Table	Segment Tree
構築	`O(NlogN)`	`O(N)`
区間最小値	`O(1)`	`O(logN)`
データの変更	不可	`O(logN)`

Sparse Table 実装が軽いため、仕組みを理解で切れば割とすんなり書けると思います。

Sparse Table の仕組み

ある配列の区間最小値を求めることを考えます。

Sparse Table はあらかじめ配列のすべての位置から2のべき乗の長さの区間についての最小値を求めておきます。

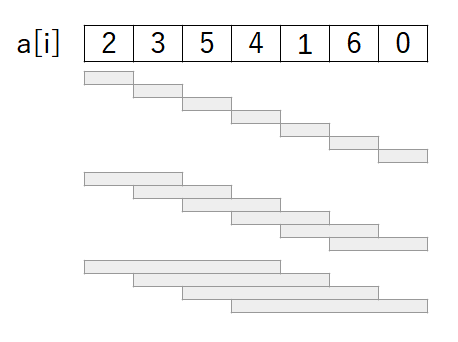
こんな感じで区間の最小値を持つテーブルを構築します。これは O(NlogN) で作ることができます。

このテーブルが構築できていれば、すべての区間について2つの区間で表すことができるようになり、事前に計算しておいた2区間の最小値の小さいほうが答えになります。

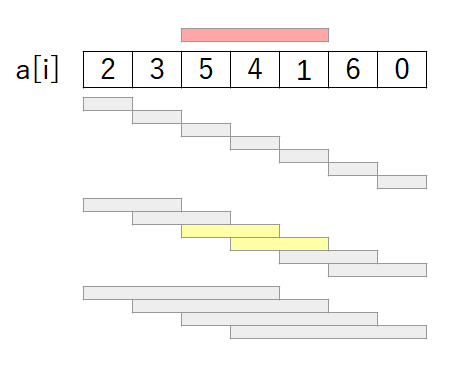
例えば上記のように長さ3の区間について答えを求めたい場合、2¹の長さの2区間をとり、その2区間の最小値を答えとできます。区間によってはこの例のように重複しますが、最小値や最大値を求める場合にはこの重複した区間が答えに影響することはありません。

では実装したコードを見てみます。

実装(C#)

わかりやすくするために long 型の配列の区間最小値を求めるような実装になっています。最大値にしても動作します。

コンストラクタで配列を渡すと初期化され、Query(l, r) で区間 [l, r) の最小値を返します。

class SparseTable
{
    private int N;
    private long[] A;
    private int[,] Table;
    private int[] LogTable;
    public SparseTable(long[] a)
    {
        A = a;
        N = a.Length;

        // N以下の数xについて、x以下で最大の2^kを求め、kを保持しておく
        // この配列を使えば log(x) が O(1) で求まる
        LogTable = new int[N + 1];
        for (int i = 2; i <= N; i++)
        {
            LogTable[i] = LogTable[i >> 1] + 1;
        }

        // Sparse Table を構築する
        CreateTable();
    }
    private void CreateTable()
    {
        // Table[i, k] は A[i]から2^k個の区間について
        // つまり A[l, l + 2^k) の最小値のインデックスを保持する
        Table = new int[N, LogTable[N] + 1];

        // 区間の長さが2^0(=1)の時の最小値はA[i]
        for (int i = 0; i < N; i++)
        {
            Table[i, 0] = i;
        }

        // 2, 4, 8 ... の順で区間の最小値を計算していく
        for (int k = 1; k <= LogTable[N]; k++)
        {
            // 開始位置をすべて調べる(i+2^k>Nの時ははみ出しているので計算しない)
            // i番目の要素から2^k個の範囲での最小値を決めたい
            for (int i = 0; i + (1 << k) <= N; i++)
            {
                // i番目の要素から2^(k-1)個の最小値
                var index1 = Table[i, k - 1];
                // i+2^(k-1)番目の要素から2^(k-1)個の最小値
                var index2 = Table[i + (1 << (k - 1)), k - 1];
                // 比較して小さくなるほうが最小値
                if (A[index1] < A[index2])
                {
                    Table[i, k] = index1;
                }
                else
                {
                    Table[i, k] = index2;
                }
            }
        }
    }

    // 区間[l, r)の最小値を返す
    public long Query(int l, int r)
    {
        var k = LogTable[r - l];
        var index1 = Table[l, k];
        var index2 = Table[r - (1 << k), k];
        return Math.Min(A[index1], A[index2]);
    }
}

コード解説

Log(x)を計算しておく

最初に、要素数をNとするときに、すべてのN以下の数xについて、x以下となる最大の2^kを求め、kをすべてテーブルに保持します。これを LogTable という名前の配列にしています。

コンストラクタの中で先に LogTable を作成しています。

// N以下の数xについて、x以下で最大の2^kを求め、kを保持しておく
// この配列を使えば log(x) が O(1) で求まる
LogTable = new int[N + 1];
for (int i = 2; i <= N; i++)
{
    LogTable[i] = LogTable[i >> 1] + 1;
}

これはコメントにある通り、N以下の数にxついて最大の2^kを求め、そのkを保持するような配列です。LogTable[3] みたいにしてアクセスることで、1と返すようになります。これはつまり (int)Math.Log2(x) が保持された配列になります。Log2の計算を毎度するのが大変なので前計算しています。

こうすることでの長さ3の区間は 2¹ の長さの区間2つで表せるということが O(1) でわかるようになります。クエリに答えるときに使うことになるので、先に計算しておきます。

Sparse Table の構築

ではメインとなる Sparse Table の構築です。この Table[i, k] が保持する値は、区間 [i, i + 2^k) の最小値のインデックスです。実際の値ではなくインデックスで保持するのに気を付けましょう。

private void CreateTable()
{
    // Table[i, k] は A[i]から2^k個の区間について
    // つまり A[l, l + 2^k) の最小値のインデックスを保持する
    Table = new int[N, LogTable[N] + 1];

    // 区間の長さが2^0(=1)の時の最小値はA[i]
    for (int i = 0; i < N; i++)
    {
        Table[i, 0] = i;
    }

    // 2, 4, 8 ... の順で区間の最小値を計算していく
    for (int k = 1; k <= LogTable[N]; k++)
    {
        // 開始位置をすべて調べる(i+2^k>Nの時ははみ出しているので計算しない)
        // i番目の要素から2^k個の範囲での最小値を決めたい
        for (int i = 0; i + (1 << k) <= N; i++)
        {
            // i番目の要素から2^(k-1)個の最小値
            var index1 = Table[i, k - 1];
            // i+2^(k-1)番目の要素から2^(k-1)個の最小値
            var index2 = Table[i + (1 << (k - 1)), k - 1];
            // 比較して小さくなるほうが最小値
            if (A[index1] < A[index2])
            {
                Table[i, k] = index1;
            }
            else
            {
                Table[i, k] = index2;
            }
        }
    }
}

まず、区間の長さが 2⁰(=1)の時の最小値はA[i]なのでこれを初期化しておきます。

次に2, 4, 8 …の順でテーブルの値を計算していきます。最初にk=0の最小値を決めているので、これを使ってk=1の時の最小値をO(1)で求めることができます。

例えば区間の長さが2¹(k=1)の最小値は、区間の長さ2⁰の値が事前に計算済なのでこれ使って、Table[i, k-1] と Table[i + (i << (k-1)), k-1] の2つの区間の最小値を比較すれば求まります。これは求めたい2のべき乗の区間をちょうど半分に割ってやることで、すでに計算済の 2^k-1 の長さの区間2つの最小値を使って計算を効率化しています。

具体的に、配列の0番目から2¹の長さの区間の最小値は、配列の0番目から長さ2⁰の区間の最小値と、配列の 0+2⁰から長さ2⁰の区間の最小値を使って求められます。図にすると以下のようなになります。

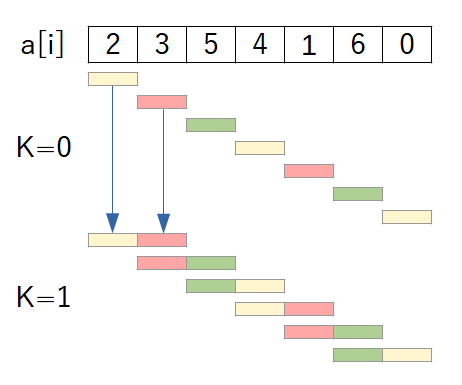
これはkが大きくなっても同様の手順で計算していくことができます。それが上のコードで実装している内容です。インデックスが配列外参照を起こさないように注意して実装してください。

クエリに答える

// 区間[l, r)の最小値を返す
public long Query(int l, int r)
{
    var k = LogTable[r - l];
    var index1 = Table[l, k];
    var index2 = Table[r - (1 << k), k];
    return Math.Min(A[index1], A[index2]);
}

区間[l, r) のクエリに答える処理です。区間は半開区間で考えます。A[l], A[l+1] .. A[r-1] の区間のことです。A[r] は含まないです。

まずこの区間の長さは r-l です。長さの区間を2つの2^kで表そうとすると、作成しておいた LogTable を参照すればよいです。

得られたkを使って、テーブルから最小値のインデックスを取り出して比較すれば答えが返せます。やっていることはテーブル構成時の手段とほぼ変わりません。

2つ目の区間を得る場合は区間の終点から2^kだけ戻った地点から長さ2^kの区間を求めればよいです。つまり Table[r - (1 << k), k] となります。

動作確認

var a = new long[] { 2, 3, 5, 4, 1, 6, 0 };
var n = a.Length;
var st = new SparseTable(a);
Console.WriteLine(st.Query(0, n)); // 0
Console.WriteLine(st.Query(0, 3)); // 2
Console.WriteLine(st.Query(1, 3)); // 3
Console.WriteLine(st.Query(4, 6)); // 1
Console.WriteLine(st.Query(5, 6)); // 6
Console.WriteLine(st.Query(4, n)); // 0

こんな感じで静的なデータに対して区間の最小値を求めることができました。

Sparse Table をライブラリを使えば、簡単に解くことができるという問題は見かけないですが、Suffix Array でLCPを求めるときに使いたくて実装しました。

AtCoder ABC 141 E – Who Says a Pun? (500 点) – けんちょんの競プロ精進記録

この記事で解説されている実装を参考に、LCPを求めてACできました。

以上。

参考URL

Suffix Array の解説と実装方法[C#][C++]

AtCoder Beginner Contest 163 に参加した記録

SparseTable の実装と解説 [C#]