AtCoder パナソニックプログラミングコンテスト2020 に参加した記録

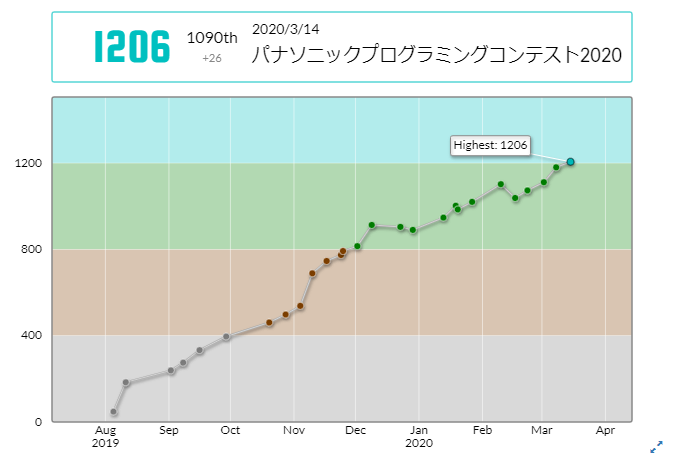
パナソニックプログラミングコンテスト2020 に参加した記録

前回のARC相当のコンテストはパスしていたので、水色チャレンジ1発目のコンテストでした。

結果ABCDの4問ACでしたが、C問題でやらかして6WAくらい重ねました。

全体的な印象として今までにない形式の問題が多かった風に思います。

やらかしたおかげでパフォーマンスは水色1420くらいでしたが、無事水色コーダーになれました!!

A – Kth Term

A – Kth Term

次の長さ 32 の数列の K 番目の項を出力してください。

1, 1, 1, 2, 1, 2, 1, 5, 2, 2, 1, 5, 1, 2, 1, 14, 1, 5, 1, 5, 2, 2, 1, 15, 2, 2, 5, 4, 1, 4, 1, 51

数列が固定なのが珍しいですが、数列をコピーしてコードに直接貼り付けてやれば解けます。

var A = new int[] { 1, 1, 1, 2, 1, 2, 1, 5, 2, 2, 1, 5, 1, 2, 1, 14, 1, 5, 1, 5, 2, 2, 1, 15, 2, 2, 5, 4, 1, 4, 1, 51 };
var K = sc.ReadInt();
var ans = A[K - 1];
Console.WriteLine(ans);

B – Bishop

B – Bishop

縦 H マス、横 W マスの盤面があります。 この盤面の左上隅のマスに角行の駒が置かれています。 駒が 0 回以上の好きな回数の移動を繰り返して到達できるマス目は何個あるでしょうか？

ただし、角行の駒は斜めに動くものとします。 より厳密には、駒が上から r1 番目、左から c1 番目のマスから上から r2 番目、左から c2 番目のマス目に動ける条件は

• r1+c1=r2+c2
• r1−c1=r2−c2

のうちちょうど一方が成立することです。たとえば、駒が図の位置にあるとき、一回で移動できる場所は赤くなっているマスです。

制約

• 1≤H,W≤10⁹
• 入力は全て整数である。

制約が10⁹なので数学的に計算して求めなければなりません。

入力例の画像を見れば計算のイメージがつくと思います。ようは大体半分くらいが塗られます。

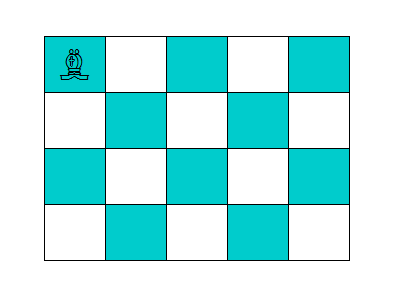
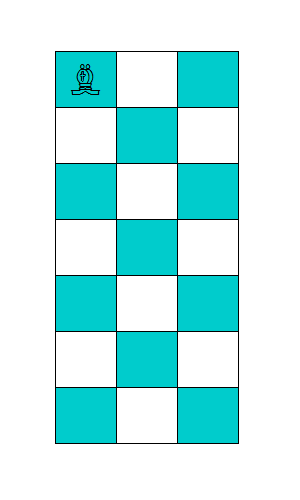
奇数の時は切り上げた数だけ塗られます。なので以下のようなコードになります。

if (H == 1 || W == 1)
{
    Console.WriteLine(1);
    return;
}
var ans = (H * W + 1) / 2;
Console.WriteLine(ans);

注意点としては列数または行数が1の時はそこから移動できないので例外的に処理します。これを見落として1WAしました。

C – Sqrt Inequality

C – Sqrt Inequality

√a+√b<√c ですか？

制約

• 1≤a,b,c≤10⁹
• 入力は全て整数である。

やらかしたC問題です。

めちゃくちゃシンプルですが a, b, c が与えられるのですが、単純に平方根を小数で計算するとWAします。たぶん誤差とかの関係だと思います。

解説PDFによると (a, b, c) = (249999999, 250000000, 999999998) みたいなケースでうまく計算できないみたいです。

この誤差問題にはすぐにたどり着いて、数式を変換して整数で扱えるようにすればよいとわかりました。

変換手順は以下の通りです。

1. 両辺を2乗する(両辺ともに正なので不等号の向きは変わらない)
   a+b+2√(ab) < c
2. 両辺から a+b を引く
   2√(ab) < c-a-b
3. 両辺を2乗する
   4ab < (c-a-b)^2

2の時点で c-a-b が負の数だと左辺が正なので絶対に成り立ちません。

3までたどり着くと入力値の整数を平方根をとらずにそのまま使えるのでよさげです。ということで実装したのが以下のコードです。

if (C - A - B <= 0)
{
    Console.WriteLine("No");
    return;
}
if (4 * A * B < Math.Pow(C - A - B, 2))
{
    Console.WriteLine("Yes");
}
else
{
    Console.WriteLine("No");
}

残念ながらこの実装ではWAになります。油断していたのが Math.Pow です。2乗するのに使っていますがこれは引数がに小数(double)になります。なので正しくは (C - A - B)*(C - A - B) と単純に2回かけなければいけません。

これを見落とした影響でWAを無駄に重ねました。

ということでACしたコードです。

var A = sc.ReadLong();
var B = sc.ReadLong();
var C = sc.ReadLong();
var x = C - A - B;
if (x <= 0)
{
    Console.WriteLine("No");
    return;
}
if (4 * A * B < x * x)
{
    Console.WriteLine("Yes");
}
else
{
    Console.WriteLine("No");
}

普段意識しない誤差に気を付けなければならないので、とってもいい問題だと思いました。

D – String Equivalence

D – String Equivalence

この問題では、英小文字からなる文字列のみを考えます。

文字列 s,t は以下の条件を満たすとき 同型 であるといいます。

• |s|=|t| である。
• 任意の i,j に対し次のいずれかが成立する。
  • si=sj かつ ti=tj
  • si≠sj かつ ti≠tj

たとえば、abcac と zyxzx は同型ですが、abcac と ppppp は同型ではありません。

文字列 s は以下の条件を満たすとき 標準形 であるといいます。

• 任意の s と同型な文字列 に対し、s≤t が成立する。ただしここで ≤ は辞書順での比較を表す。

たとえば、abcac は標準形ですが、zyxzx はそれより辞書順で小さい　abcac と同型のため標準形ではありません。

整数 N が与えられます。 長さ N の標準形の文字列を全て、辞書順で昇順で出力してください。

制約

• 1≤N≤10
• 入力は全て整数である。

C問題が解けずに焦っていたので、先にD問題に手を付けました。この問題は10分程度で解けました。

いろいろ問題文はややこしいことを言っていますが、まず気が付くのは使う文字は最大でN文字だということです。

次に気が付いたのは文字の違いだけが重要だということです。異なれば辞書順で一番小さい文字を使わなければなりません。つまり a を使ったことがないのに b や c を使ってはいけないということです。

なのでそれを踏まえてDFSで実装すればOKです。

これまでに使った最も大きい文字を管理しておき、その次の文字まで使えるようにして全探索します。

static void Main(string[] args)
{
    N = sc.ReadInt();

    // 使える文字種を用意しておく
    A = new char[N];
    for (int i = 0; i < N; i++)
    {
        A[i] = (char)('a' + i);
    }

    // 最終出力の文字配列
    var s = new char[N];

    Rec(0, s, 0);
}
static char[] A;
static int N;
static void Rec(int n, char[] s, int maxc)
{
    if (n == N)
    {
        var ans = string.Join("", s);
        Console.WriteLine(ans);
        return;
    }
    // n文字目に使う文字を全探索する
    // 使えるのはこれまでに使用した最大文字+1までのどれか
    for (int i = 0; i <= maxc; i++)
    {
        s[n] = A[i];
        Rec(n + 1, s, i == maxc ? maxc + 1 : maxc);
    }
}

とりあえずこれでACしました。Cが解けてない状態でしたが冷静にACできてよかったです。

このあとC問題も落ち着いて対応したらいけました。

E – Three Substrings

E – Three Substrings

E問題は40分くらい時間があったのですが、何も思いつきませんでした。

今回のコンテストで AtCoder 開始時に目標にしていた水色コーダーになれたのでうれしいです。せっかくなので次は「水色コーダーになるまでにやったこと」みたいなブログを書いてみようと思います。

現状青までは何とかなりそうな気がしないでもないので続けて頑張ろうと思います。始めたての時のD問題より今見るE問題のほうがまだ手に負えそうなきがするので青まではたどり着きたいなと思ってます。

たぶんE問題が解ければ青パフォーマンス安定すると思うので頑張ります。

以上。