19 評価プロセス(前置式 “-“, “!”) [オリジナル言語インタプリタを作る]

真偽値

整数リテラルの評価に続いて真偽値リテラルの評価を実装します。とはいえやることは整数リテラルの評価とほぼ変わりません。

テストの作成

まずはテストを作成します。

[TestMethod]
public void TestEvalBooleanExpression()
{
    var tests = new(string, bool)[]
    {
        ("true;", true),
        ("false", false),
    };

    foreach (var (input, expected) in tests)
    {
        var evaluated = this._TestEval(input);
        this._TestBooleanObject(evaluated, expected);
    }
}

private void _TestBooleanObject(IObject obj, bool expected)
{
    var result = obj as BooleanObject;
    if (result == null)
    {
        Assert.Fail("object が Boolean ではありません。");
    }

    Assert.AreEqual(expected, result.Value);
}

整数リテラルのテストと同じような内容なので説明は割愛します。

EvalBooleanLiteral()

では真偽値リテラルの評価を実装します。

public class Evaluator
{
    public BooleanObject True = new BooleanObject(true);
    public BooleanObject False = new BooleanObject(false);

    public IObject Eval(INode node)
    {
        switch (node)
        {
            // ..
            case BooleanLiteral booleanLiteral:
                return booleanLiteral.Value ? this.True : this.False;
        }
        return null;
    }
    // ..
}

整数リテラルト同じように Eval() の中で条件分岐を追加します。そしてリテラルの値によって BooleanObject を返します。

注意すべきは都度 BooleanObject を生成するのではなく、あらかじめ生成しておいた True, False を必要に応じて返すようにしているということです。

Booleanは true/false のいずれかしかありえません。であれば必要になるたびにオブジェクトを生成するという無駄なコストを払うよりも、あらかじめ生成しておいたオブジェクトを使いまわす方が賢明です。

これで真偽値リテラルの評価は完了です。

前置演算式 !

次は前置演算式(!)の評価です。

作成中のプログラミング言語 Gorilla では !5 のような式が有効です。つまり真偽値以外の型の時、true/false どちらで評価するかを決めなければなりません。

真偽値以外のすべての型は truthly として扱います。0 も truthly です。また Null については例外的に falsely として扱います。

テストの作成

まずはテストを作成します。テストケースでどのように判定されるかを確認してください。

[TestMethod]
public void TestEvalBangOperator()
{
    var tests = new(string, bool)[]
    {
        ("!true", false),
        ("!false", true),
        ("!5", false),
        ("!!true", true),
        ("!!!true", false),
        ("!!5", true),
    };

    foreach (var (input, expected) in tests)
    {
        var evaluated = this._TestEval(input);
        this._TestBooleanObject(evaluated, expected);
    }
}

2重3重の否定もテストしています。Null のリテラルは存在しないのでまだテストできません。これを通せるように実装していきます。

実装

public class Evaluator
{
    public BooleanObject True = new BooleanObject(true);
    public BooleanObject False = new BooleanObject(false);
    public NullObject Null = new NullObject();

    public IObject Eval(INode node)
    {
        switch (node)
        {
            // ..
            case PrefixExpression prefixExpression:
                var right = this.Eval(prefixExpression.Right);
                return this.EvalPrefixExpression(prefixExpression.Operator, right);
        }
        return null;
    }
    // ..
    public IObject EvalPrefixExpression(string op, IObject right)
    {
        switch (op)
        {
            case "!":
                return this.EvalBangOperator(right);
        }
        return this.Null;
    }

    public IObject EvalBangOperator(IObject right)
    {
        if (right == this.True) return this.False;
        if (right == this.False) return this.True;
        if (right == this.Null) return this.True;
        return this.False;
    }
}

まず、Nullについても真偽値と同じように、Nullが評価されるたびにオブジェクトを生成するのは無駄なので1つのインスタンスを定義しておきます。

次に前置演算式の評価を行う分岐を追加し、そこから前置演算式の評価を行う処理 EvalPrefixExpression を呼び出します。そして右辺の値(!5 なら 5)を評価し、その値に対して演算子による評価を行います。

EvalBangOperator() は右辺の値を引数で貰い受け、その値の否定を BooleanObject で返します。先ほど決めたとおり、このインタプリタでは 真偽値以外のすべての型はTrueと評価されます。Nullについては特別にFalseと評価します。したがってここではそれぞれを否定した結果をそれぞれ返しています。

なお True, False, Null はそれぞれ単一のインスタンスしか存在しないはずなので “==” で等価判定しています。いちいち内部の値を取り出して判定する必要も、型変換の必要もないのです。

ここまでのソース

mntm0/Gorilla at 812e5c19faf70deda8e7e1d66e2e58d6bb53b942

前置演算子 –

同じく前置演算子のマイナス “-” についても評価を実装しましょう。

テストの作成

新しくテストを作成する必要はなく、TestEvalIntegerExpression() にテストケースとしてマイナスの数を追加して対応します。

[TestMethod]
public void TestEvalIntegerExpression()
{
    var tests = new(string, int)[]
    {
        ("1", 1),
        ("12", 12),
        ("-1", -1),
        ("-12", -12),
    };
    // ..
}

実装

public class Evaluator
{
    // ..
    public IObject EvalPrefixExpression(string op, IObject right)
    {
        switch (op)
        {
            // ..
            case "-":
                return this.EvalMinusPrefixOperatorExpression(right);
        }
        return null;
    }
    // ..
    public IObject EvalMinusPrefixOperatorExpression(IObject right)
    {
        if (right.Type() != ObjectType.INTEGER) return this.Null;

        var value = (right as IntegerObject).Value;
        return new IntegerObject(-value);
    }
}

前置演算子の評価に分岐を追加し、マイナス演算子の場合の評価を呼び出します。

整数であればそれをマイナスにしたオブジェクトを生成します。

これでOKです。

ここまでのソース

mntm0/Gorilla at 1b1b472344ace159e7ca679162525991b38d5335

まとめ

前置演算子の評価を実装しました。これで以下のようにREPLで評価された結果を確認することができます。

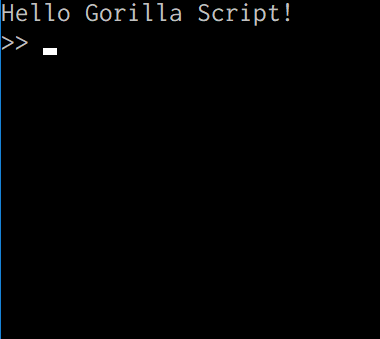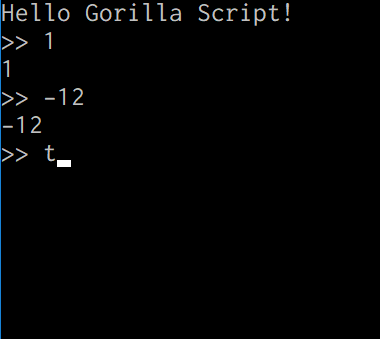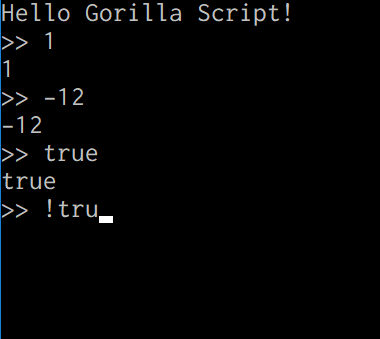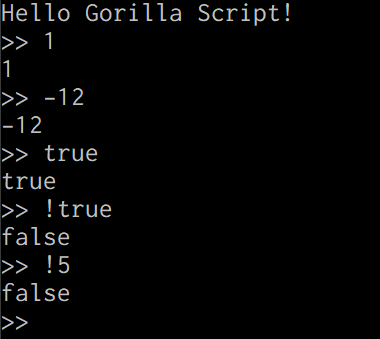
次回は中置演算式の評価を実装します。これが完成するとRELPが四則演算のできる電卓みたいになります。

以上。