評価プロセス
ここまでで字句解析、構文解析と終りました。ようやくREPLでいうところの E(Eval, 評価)に移ることができます。
インタプリタにおける評価のプロセスは、プログラムがどのように動作するかを定義する必要があります。
例えば以下のプログラムを例に考えます。
let num = 5;
if (num) {
return 1;
} else {
return 0;
}
これが 1 を返すのか 0 を返すのかは、各プログラミング言語の評価の仕方によって異なります。5 という整数を truthly として扱うか falsely として扱うか、この違いがあります。あるいは、そもそもifの条件式には真偽値以外を許さない言語もあります。
次の例はどうでしょう。
let foo = fn() { 0 }
let bar = fn() { 1 }
add(foo(), bar());
関数の呼び出し式の引数に、関数の呼び出し式を指定しています。foo() と bar() どちらが先に評価されるでしょうか。なんとなく先頭の引数から順番に評価されそうですが、これも実装により異なります。
遅延評価を実装する言語だと、必要になるまで評価が行われないということもあります。
評価のプロセスを実装することは、プログラミング言語の動作を定義づけることを意味します。評価の方法はさまざま考えられますが、これまで通り基本的にはシンプルな方法を採用していきます。
tree-walking型インタプリタ
どのようにコードを評価するのでしょうか。私たちにはASTがあります。したがってこのASTを評価する方法を考えます。
構文解析器によって得られたASTをどのように評価するのかという点でいくつかの選択肢があります。
ASTの最もわかりやすい利用方法は、ASTの各ノードを巡りながら評価していく方法です。これを tree-walking型インタプリタ と呼びます。これがインタプリタの原型です。
ノードを順に巡りながら評価する方法は、直感的に処理が遅いのではないかと思われますがその通りです。
より速く動作させるためにASTを最適化によって書き換えたり、別の中間表現に置き換えたりする方法もあります。また、先にノードを巡ってバイトコードを生成してから仮想マシンで実行する方法もあります。実行直前に仮想マシンで機械語に変換してから実行するJITと呼ばれる方法も有名です。
これらの方法を組み合わせたバリエーションが考えられますが、どのような性能や移植性を要求するかで選択は変わってきます。今回はもっとも基本にある tree-walking型 を採用します。シンプルかつ分かりやすい方法です。
Wikipedia の記事によると 抽象構文木インタプリタとも呼ばれるようです。ここにある通り、プログラミング言語 Ruby では、バージョン 1.8 まではこの方法を採用しています。そしてバージョン 1.9 以降ではバイトコードを生成するインタプリタに変更し、性能向上を果たしたとあります。
つまり tree-walking型インタプリタ 由緒正しき方法だといえるでしょう。ということで採用決定です。
tree-walking型 のイメージ
以前式の解析で例に出した 1 + 2 * 3 という式についてのASTを用いて tree-walking型の評価をイメージしてみましょう。
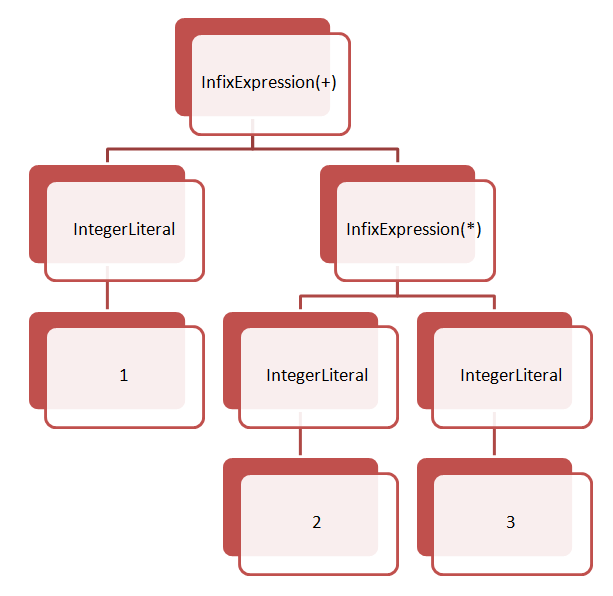
このASTを評価するにはルートから順に評価していきます。そしてルートから子ノードを順に評価していくという流れです。具体的には以下のようになります。
- 足し算を評価します。(1+6=7)
- 左辺を評価します。(=1)
- 整数リテラル 1 を評価します。
- 右辺を評価します。(2*3=6)
- 掛け算を評価します。(2)
- 左辺を評価します。(=2)
- 整数リテラル 2 を評価します。
- 右辺を評価します。(=3)
- 整数リテラル 3 を評価します。
- 左辺を評価します。(=2)
- 掛け算を評価します。(2)
- 左辺を評価します。(=1)
ルートから順に各ノードを評価し、各ノードは必要に応じて子ノードの評価を呼び出しますそれによってどんどん根に向かって再帰的に評価が進み、最終的な評価結果が得られるようになります。
ここからわかることは、全てのASTノードは評価することによってなにがしかの値を生成します。つまり INode を引数にした Eval() を実装しなければならないということです。(後述)
なんとなく tree-walking型 の評価イメージはつかめたと思います。しかしこの評価関数 Eval() はどのような値を返せばよいのでしょうか。
オブジェクトと型
各ノードが Eval() を実装することで評価結果を得るとわかりましたが、この評価結果はどのような値でしょうか。例では整数の演算式を挙げましたが、実際にはいくつかの式があり、どのような値をとるかはわかりません。
したがって、まずはインタプリタが実装するオブジェクトの内部表現を定義する必要があります。ASTを評価した際にメモリ上に生成される値の表現方法、Eval() が返す型を決めましょう。
インタプリタにおける値の内部表現の定義は多種多様です。これはインタプリタの実装に用いるホスト言語の表現にある程度依存するためです。ホスト言語の型をラップした独自の型を用いることもできますし、そのまま利用することも考えられます。あるいはホスト言語に用意されていない方を独自に定義することも考えられます。
要求される処理速度によっては高価なオブジェクトシステムを用いることはできないこともあります。
もちろんここでの実装はもっとも単純かつシンプルな方法を用います。インターフェース IObject を定義し、これを実装する型をこのインタプリタでの内部表現とします。
オブジェクトの定義
ということでまずは IObject を定義します。
Objects/IObject.cs
namespace Gorilla.Objects
{
public interface IObject
{
ObjectType Type();
string Inspect();
}
public enum ObjectType
{
INTEGER,
BOOLEAN,
NULL,
}
}
保持するのは、このオブジェクトのインタプリタ上での型 ObjectType を返す Type() と、この値の文字列表現を返す Inspect() です。Inspect() は評価結果を表示するときに使います。
ObjectType は 整数型と真偽値型があります。整数リテラルで用意した型ですね。NULLはリテラルの定義がありませんが、たとえば関数の呼び出し時に何も値が評価されない場合など、NULLにならざるを得ない状況がありますしたがってNULLを表すオブジェクトも用意できるようにします。
整数や真偽値の値は IObject を実装する各オブジェクトで保持します。これは内部データのサイズが違うため、1つの共通フィールドで管理するのが難しいためです。それぞれ別で持てばOKです。
これで Eval() が返す型を定義できました。続けてこれを実装する各オブジェクトを定義していきます。
整数
Objects/IntegerObject.cs
namespace Gorilla.Objects
{
public class IntegerObject : IObject
{
public int Value { get; set; }
public IntegerObject(int value) => this.Value = value;
public string Inspect() => this.Value.ToString();
public ObjectType Type() => ObjectType.INTEGER;
}
}
整数リテラルのASTノードを評価する場合、この IntegerObject を生成します。
このオブジェクトで整数値をラップして保持します。Type() は整数型を表す ObjectType.INTEGER を返します。
これだけです。
真偽値
Objects/BooleanObject.cs
namespace Gorilla.Objects
{
public class BooleanObject : IObject
{
public bool Value { get; set; }
public BooleanObject(bool value) => this.Value = value;
public string Inspect() => this.Value ? "true" : "false";
public ObjectType Type() => ObjectType.BOOLEAN;
}
}
真偽値も整数型と違いはありません。bool型の値をラップしています。
NULL
Objects/NullObject.cs
namespace Gorilla.Objects
{
public class NullObject : IObject
{
public string Inspect() => "null";
public ObjectType Type() => ObjectType.NULL;
}
}
Null値もオブジェクトとして保持しますが、どの値もラップしません。
評価器のテスト
評価器を実装する前に先にテストを書きましょう。最初に実装できるようにするのは整数リテラルの評価です。
つまり 1 と入力したら 1 と評価されるという至極単純な評価です。
EvaluatorTest.cs
using Gorilla.Evaluating;
using Gorilla.Lexing;
using Gorilla.Objects;
using Gorilla.Parsing;
using Microsoft.VisualStudio.TestTools.UnitTesting;
namespace UnitTestProject
{
[TestClass]
public class EvaluatorTest
{
[TestMethod]
public void TestEvalIntegerExpression()
{
var tests = new(string, int)[]
{
("1", 1),
("12", 12),
};
foreach (var (input, expected) in tests)
{
var evaluated = this._TestEval(input);
this._TestIntegerObject(evaluated, expected);
}
}
private IObject _TestEval(string input)
{
var lexer = new Lexer(input);
var parser = new Parser(lexer);
var root = parser.ParseProgram();
var evaluator = new Evaluator();
return evaluator.Eval(root);
}
private void _TestIntegerObject(IObject obj, int expected)
{
var result = obj as IntegerObject;
if (result == null)
{
Assert.Fail("object が Integer ではありません。");
}
Assert.AreEqual(expected, result.Value);
}
}
}
_TestEval() はソースコードを入力値として引数で渡し、これを評価した結果を返すヘルパ関数です。内部的には字句解析、構文解析の順に進めてASTを取得し、これを評価器に渡して評価しています。評価器はまだ作成していないのでコンパイルエラーになります。
_TestIntegerObject() は、評価されたオブジェクトが期待する整数値かどうかをテストするヘルパ関数です。
TestEvalIntegerExpression() はこれらを呼び出すことで与えられたテストケースの入力が、正しく評価されているかを確認しています。
まだ評価器 Evaluator が実装されていないのでこのテストはコンパイルすらできません。
評価器の実装
テストを通すべく、評価器 Evaluator の実装に移ります。
using Gorilla.Ast;
using Gorilla.Ast.Expressions;
using Gorilla.Ast.Statements;
using Gorilla.Objects;
using System.Collections.Generic;
namespace Gorilla.Evaluating
{
public class Evaluator
{
public IObject Eval(INode node)
{
switch (node)
{
case IntegerLiteral integerLiteral:
return new IntegerObject(integerLiteral.Value);
}
return null;
}
}
}
評価するメソッド Eval() のシグネチャは以下の通りです。
IObject Eval(INode node)
引数で評価するASTのノードを渡します。そしてそのASTノードを評価した結果を先ほど定義した IObject で返します。
全てのASTノードは INode を実装します。したがってそれぞれのノードに合わせて異なる評価方法を採る必要があります。そのため Eval() では、渡されたノードの型に応じて処理を分岐します。
IntegerLiteral が渡された場合 IntegerObject を生成して返すようにすればOKです。
これでうまくいきそうですが、まだテストは通りません。なぜか。思い出してほしいのは、構文解析器は Root からなる1つの木構造を生成するという点です。
つまり ‘1’ という入力は、Root->Statements[0]->ExpressionStatement->IntegerLiteral という階層で定義されます。
Rootノードの下に複数の文(この場合1つの式文)があり、その式文の中の式が整数リテラルとなります。このようにノードは子ノードを持つ形で構成されます。このとき Root を評価するにはすべてのノードを順に評価していかなければなりません。
したがってテストをうまく通すには、少なくとも Root と ExpressionStatement に対応した評価方法も合わせて実装する必要があります。
public class Evaluator
{
public IObject Eval(INode node)
{
switch (node)
{
//文
case Root root:
return this.EvalStatements(root.Statements);
case ExpressionStatement statement:
return this.Eval(statement.Expression);
// 式
case IntegerLiteral integerLiteral:
return new IntegerObject(integerLiteral.Value);
}
return null;
}
public IObject EvalStatements(List<IStatement> statements)
{
IObject result = null;
foreach (var statement in statements)
{
result = this.Eval(statement);
}
return result;
}
}
これが最初の評価器です。テストも通ります。何をやっているのでしょうか。
まず Root の評価時には、すべての文について評価処理を行います。EvalStatements() に切り出している部分ですね。Root直下のすべての文について Eval() を呼び出して結果を受け取るようにします。
Root の評価結果は最後に評価された文の結果を使います。それ以外の評価結果は無視しますが、評価自体はすべての文に対して行わないとなりません。
ExpressionStatement の評価は中身の式を評価することで得られます。1 という式文の式は整数リテラル 1 です。つまり整数オブジェクトが結果として変えることになります。
こうして Root 以下すべてのノードが再帰的に評価されることで、最終的なASTの評価結果が得られることになります。
これが評価器の基本形になります。あとはこの Eval() を拡張していくことで式や関数呼び出しの評価が可能になります。
ここまでのソース
https://github.com/mntm0/Gorilla/commit/9d0f00681a09feb978432996279a1f1660b2ef6a
REPL の実装
ようやく評価器の最初のバージョンが完成しました。REPLに組み込んで評価された結果を表示できるようにしましょう。
短いコードなので全文を載せます。
Repl.cs
using Gorilla.Evaluating;
using Gorilla.Lexing;
using Gorilla.Parsing;
using System;
namespace Gorilla
{
public class Repl
{
const string PROMPT = ">> ";
public void Start()
{
while (true)
{
Console.Write(PROMPT);
var input = Console.ReadLine();
if (string.IsNullOrEmpty(input)) return;
var lexer = new Lexer(input);
var parser = new Parser(lexer);
var root = parser.ParseProgram();
if (parser.Errors.Count > 0)
{
foreach (var error in parser.Errors)
{
Console.WriteLine($"\t{error}");
}
continue;
}
var evaluator = new Evaluator();
var evaluated = evaluator.Eval(root);
if (evaluated != null)
{
Console.WriteLine(evaluated.Inspect());
}
}
}
}
}
ToCode() でASTを表示していた箇所を、評価器による評価結果の内容に置き換えています。IObjectの文字列表現は Inspect() で取得します。
これでようやく 1 と入力して 1 と表示されるインタプリタとREPLが完成しました!
まとめ
ここまでのソース
mntm0/Gorilla at 5bafdecb49d0217a1e37729f09d990e25ebd328d
数字を入力して数字が表示されるだけですが、大量の実装を行ってきました。しかしここからが楽しいところです。
次回は真偽値リテラルと前置演算式(!)の評価を行います。
以上。
![18 評価プロセス(リテラル) [オリジナル言語インタプリタを作る]](https://webbibouroku.com/wp-content/uploads/eye_gorilla.png)




コメントを書く