Pratt 構文解析
Pratt構文解析 という手法で式の構文解析を実装してきました。ここまでの実装で演算子の優先度を考慮したうえで、正しいASTノードを構築できるようになりました。
しかし実装がうまくいったのはテストを作成することで確認できましたが、詳しい説明は端折っていました。詳しい理論はぶっちゃけわからないのですが、どのように動作するかを見ていこうと思います。
VSにのデバッグ機能は優秀ですので、ブレークポイントを張りつつ、ステップ実行してみていくとより分かりやすいです。
A + B + C
例えば A + B + C という式について考えてみます。この式は ((A + B) + C) のようなASTノードになります。より優先度の高い中置演算式については、より深い階層のノード(括弧の中)に配置されます。
このASTは、中置演算子”+”が2つあるので InfixExpression ノードを2つもっていることがわかります。
図にすると以下のようになります。
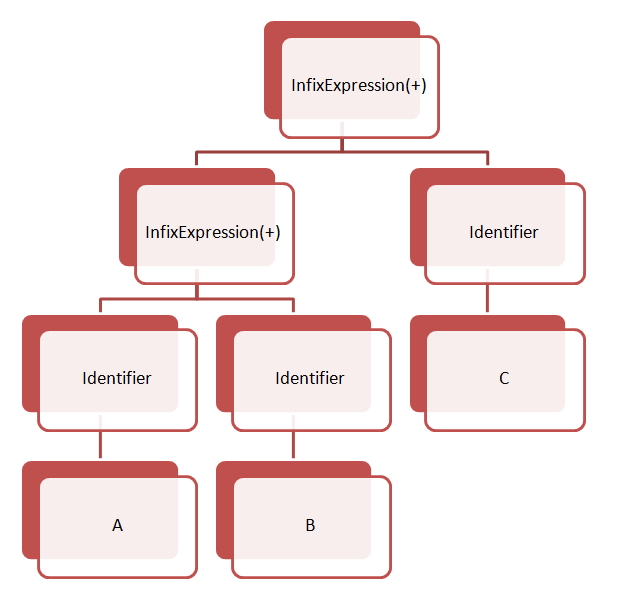
これが構文解析器の出力するASTノードです。
問題はこのノードがどのようにして作られるかです。
コード再掲
重要な部分のコードを以下に示します。
public IExpression ParseExpression(Precedence precedence)
{
this.PrefixParseFns.TryGetValue(this.CurrentToken.Type, out var prefix);
if (prefix == null)
{
this.AddPrefixParseFnError(this.CurrentToken.Type);
return null;
}
var leftExpression = prefix();
while (this.NextToken.Type != TokenType.SEMICOLON
&& precedence < this.NextPrecedence)
{
this.InfixParseFns.TryGetValue(this.NextToken.Type, out var infix);
if (infix == null)
{
return leftExpression;
}
this.ReadToken();
leftExpression = infix(leftExpression);
}
return leftExpression;
}
public IExpression ParseInfixExpression(IExpression left)
{
var expression = new InfixExpression()
{
Token = this.CurrentToken,
Operator = this.CurrentToken.Literal,
Left = left,
};
var precedence = this.CurrentPrecedence;
this.ReadToken();
expression.Right = this.ParseExpression(precedence);
return expression;
}
このコードで A + B + C がどのように解析されるか、順を追ってみていきます。
なお現在のトークンを下線で示すことにします。最初に ParseExpression() が呼ばれるときの現在のトークンは以下のようになります。
A + B + C
最初に ParseExpression() が呼び出されるとき 優先度は LOWEST です。
ここでまず行われるのは現在のトークン(識別子”A”)に関連付けられた前置解析関数(prefix)が存在しているかどうかです。これは識別子解析関数が定義されており、呼び出すと識別子ASTノードが生成されます。これがひとまず左辺の式となります。
var leftExpression = prefix();
この部分です。
問題は次のwhile文です。まだ現在のトークンは変わらず “A” のままですので、次のトークンの種類は “+” です。このトークンの優先度はSUMでありLOWESTより高く設定されています。
ここで一度優先度の定義を確認しておきます。
public enum Precedence
{
LOWEST = 1,
EQUALS, // ==
LESSGREATER, // >, <
SUM, // +
PRODUCT, // *
PREFIX, // -x, !x
CALL, // myFunction(x)
}
LOWEST が 1 で一番低く、SUM は 4 となります。while文の中身を再び見てみましょう。
while (this.NextToken.Type != TokenType.SEMICOLON
&& precedence < this.NextPrecedence)
{
this.InfixParseFns.TryGetValue(this.NextToken.Type, out var infix);
if (infix == null)
{
return leftExpression;
}
this.ReadToken();
leftExpression = infix(leftExpression);
}
while文の最初のループを考えると、まだトークンの読み込み位置は変わりありません。
A + B + C
したがって次のトークンは演算子”+”になります。”+”に関連づく解析関数を辞書 InfixParseFns から取り出しています。ここで ParseInfixExpression() が得られます。
ここで注意すべきはいきなり得られた解析関数を呼び出すのではなく、現在のトークンを読み飛ばして対応する中置演算子に進めてから、解析関数を呼び出します。呼び出す際は先ほど解析しておいた左辺の識別子”A”を引数で渡しています。
当然解析済の部分なので、トークンを読み進めたということです。
public IExpression ParseInfixExpression(IExpression left)
{
var expression = new InfixExpression()
{
Token = this.CurrentToken,
Operator = this.CurrentToken.Literal,
Left = left,
};
var precedence = this.CurrentPrecedence;
this.ReadToken();
expression.Right = this.ParseExpression(precedence);
return expression;
}
では、この ParseInfixExpression() では何が行われるでしょうか。呼び出し時のトークン列の読み込み位置は以下の通りです。
A + B + C
中置解析関数 ParseInfixExpression() が呼ばれるとき、中置演算子トークンが現在のトークンとなっています。
引数で渡された左辺と現在のトークンから得られる中置演算子をASTノードに持たせます。
ここで演算子の右側の式を解析するのですが、その前に演算子の優先度を取得します。取得後、演算子トークンは様子見なので読み飛ばします。
そして右辺の解析処理を呼び出します。先ほど取得した中置演算子の優先度を引数で渡します。
expression.Right = this.ParseExpression(precedence);
右辺の解析で再び ParseExpression() が呼ばれています。呼び出し時の現在のトークンは以下の通りです。
A + B + C
この時の ParseExpression() の役割は B + C を解析するときと同じような動作です。違いは引数で渡される優先度が異なる点です。
左辺として識別子”B”が生成されます。
そして1度目呼び出し時の処理との違いがwhile文で出てきます。
この時点のトークンの優先度はSUM(=4)です。引数で与えられた優先度と同じですね。ということはwhile文の中身に処理が進まなくなり、左辺の式(識別子”B”)がそのまま返ることになります。
ということは InfixExpression() が返すASTは以下の図のようになります。
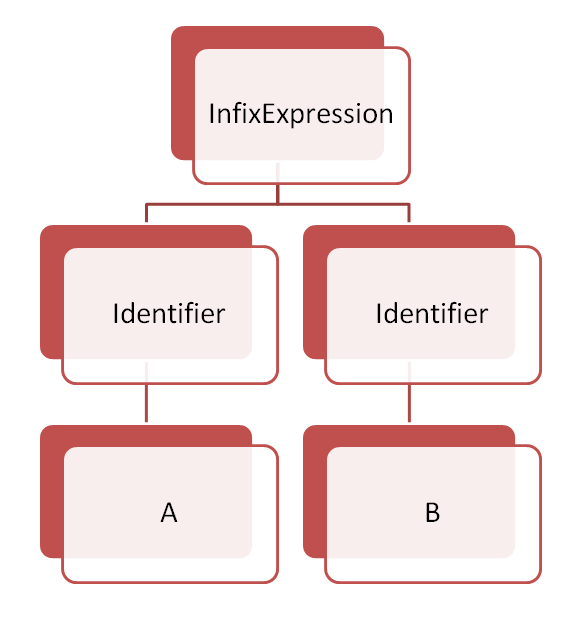
これが一番外側の呼び出し元である ParseExpression() のwhile文末尾に戻ってきます。
while (this.NextToken.Type != TokenType.SEMICOLON
&& precedence < this.NextPrecedence)
{
this.InfixParseFns.TryGetValue(this.NextToken.Type, out var infix);
if (infix == null)
{
return leftExpression;
}
this.ReadToken();
leftExpression = infix(leftExpression);
}
1度目のループが終わりました。再びwhile文の条件判定ですが、現在のトークンは以下の通りです。
A + B + C
まだ “B” の位置のままです。初回呼び出し時の ParseExpression() の引数は LOWEST です。したがって次のトークンの種類が”+”であり、優先度がより高いため次のループ処理に進むことができます。
その後、次のトークン”+”に進み、解析関数が呼ばれます。この時の引数として先のループで生成した上で示したの図のノードが左辺の式として渡されます。
あとはこの左辺の式 (A + B) と “C” が “+” を演算子としてノードとしてASTノードを構成することになります。これで以下のような図になります。

優先度(Precedence)の意味
ここで考えておきたいのが優先度の意味についてです。優先度は2つの場所で登場します。
ParseExpression() の引数とwhile文の条件式に出てくる次のトークンの優先度です。これらを比較することで優先度を考慮したうえでASTの各ノードをうまく振り分けています。
ではそれぞれ優先度はどのような意味を持つのでしょうか。これは現在の演算子から見て、左右どちらに引き付けられるか、その強さを表しています。これを結合力と呼びます。
引数の優先度がは右への結合力、次のトークン種類の優先度は左への結合力を意味しています。
つまり、次のトークン種類の優先度が高い(左結合力が高い)場合、左側の階層に結合するため左の階層がより深くなります。逆に引数の優先度が高い場合、右の階層に結合するため右の階層がより深くなります。
例えば A + B * C を考えると (A + (B * C)) のようなASTになります。
B以下の式が解析されるときの引数の優先度は SUM(=4) つまり”+”の右結合力が4です。左結合力は次のトークンが”“なので PRODUCT(=5) となります。右結合力 > 左結合力なので “+” が右に位置する式を引き寄せる力よりも “” が左にある式を吸い付ける力が強くなります。
となると “” 側に強い結合が働くため `(B C)` が深い階層で組み合わされることになります。これがwhile文の中で繰り返し左結合力の強い限り右辺の式を入れ子にしている部分の意味になります。
その逆のパターン A + B == C も見てみましょう。”==” の演算子が持つ優先度は2であり、非常に低くなっています。これは “==” の左結合力が低いことを意味します。つまり “B” と “C” の結合が弱いということです。
逆に “+” の右結合力は4であり、”==”の引き付ける力よりも強いため “A” と “B” はより強く結びつき、((A + B) == C) ような結果になります。
注意すべきはなのは、左結合力が強いと左側の要素を引き付けて右に持ってくるので右辺の式の階層が深くなり、その逆は左辺の式の階層が深くなるということです。ややこしいですが。
まとめると、演算子が複数ある場合、その演算子の引き付ける力を比較し、より強いほうの演算子の式が深く階層を作るということです。その判定を行っているのがwhile文の条件式です。
式の解析の謎は解けたでしょうか?
これで式の解析はひとまず終了です。そして構文解析器のパートもあとわずかです。もういくつかの機能を拡張し、それで構文解析器は完了とします。
次回は真偽値リテラルやグループ化された式の解析を行います。
以上。
![11 Pratt 構文解析 [オリジナル言語インタプリタを作る]](https://webbibouroku.com/wp-content/uploads/eye_gorilla.png)




コメントを書く