[C#] ダイクストラ法で最短経路を見つけるための実装方法

ダイクストラ法とは

ダイクストラ法 – Wikipedia

ダイクストラ法とは、Wikipedia によると次のように説明されます。

ダイクストラ法（だいくすとらほう、英: Dijkstra’s algorithm）はグラフ理論における辺の重みが非負数の場合の単一始点最短経路問題を解くための最良優先探索によるアルゴリズムである。

ある点からの最短経路を求めるときに使用されるアルゴリズムです。

二分ヒープで実装した PriorityQueue を使用することで計算量 O((E+V)logV) となります。Eが辺、Vが頂点です。

アルゴリズム

ダイクストラのアルゴリズムの流れは以下の通りです。

1. 開始地点を最短経路候補としてキューに入れる。
2. 最短経路の候補から最も小さい値(コスト)を持つ頂点を取り出す。要素が存在しない場合は 6 に進む。
3. 取り出した頂点までの経路(コスト)を最短経路として確定する。
   • ただし、すでに確定した経路よりも大きい値の場合は無視する。
4. 確定した地点から直接つながる頂点に対して、経路(コスト)を計算する。
   • すでに計算済のコストと比較して小さい場合、キューに追加し、コストを記録する。それ以外の場合は無視する。
5. 2 に戻る。
6. 開始地点からすべての頂点への最短経路が確定したので終了する。

開始地点からの距離がより小さい頂点から順番に確定させていきます。よって候補となる頂点から最も小さい値を効率よく取り出せるように優先度付きキューを利用します。単純に実装するとすべての頂点をループして確認する必要があるので O(V²) となってしまいます。

ちなみにすべての辺のコストが1(一定)の場合、これは幅優先探索と同じになります。コストが同じなら見つけたものから順番に取り出すだけでよいということです。迷路の最短経路探索とかで見るやつです。

辺のコストがそれぞれで異なる場合は優先度をつけて確定させる順番を決めてやる必要があります。

動きのイメージはこんな感じです。

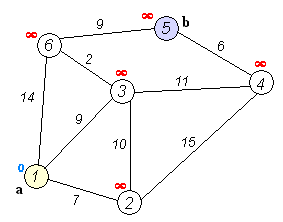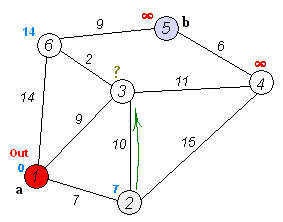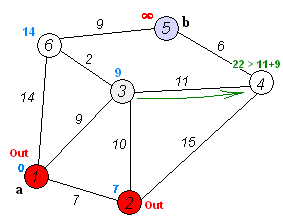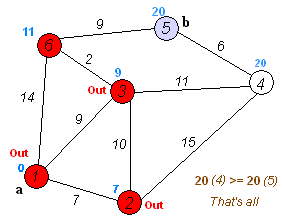
実装例

C# で実装してみます。

[C#][VB] 優先度付きキューを実装する方法 │ Web備忘録

優先度付きキューは上のページで実装したものを使いますが、ここではコードが長くなるので省略します。

class Dijkstra
{
    public int N { get; set; }
    public List<Edge>[] G { get; set; }
    public Dijkstra(int n)
    {
        this.N = n;
        this.G = new List<Edge>[N];
        for (int i = 0; i < N; i++)
        {
            this.G[i] = new List<Edge>();
        }
    }
    // a から b につながる辺を追加する
    public void Add(int a, int b, long cost = 1)
    {
        this.G[a].Add(new Edge(b, cost));
    }

    // 単一始点の最短経路を求める
    public long[] GetMinCost(int start)
    {
        // 最短経路(コスト)を格納しておく配列(すべての頂点の初期値をINFにしておく)
        var cost = new long[N];
        for (int i = 0; i < N; i++) cost[i] = long.MaxValue;
        cost[start] = 0;

        // 未確定の頂点を格納する優先度付きキュー(頂点とコストを格納)
        var q = new PriorityQueue<P>(this.N, false);
        q.Enqueue(new P(start, 0));

        // 未確定の頂点があればすべて確認する
        while (q.Count > 0)
        {
            var p = q.Dequeue();
            // すでに記録されているコストと異なる(より大きい)場合、無視する。
            if (p.Cost != cost[p.A]) continue;

            // 取り出した頂点を確定する。
            // 確定した頂点から直接辺でつながる頂点をループ
            foreach (var e in this.G[p.A])
            {
                // すでに記録されているコストより小さいコストの場合
                if (cost[e.To] > p.Cost + e.Cost)
                {
                    // コストを更新して、候補としてキューに入れる
                    cost[e.To] = p.Cost + e.Cost;
                    q.Enqueue(new P(e.To, cost[e.To]));
                }
            }
        }

        return cost;
    }

    // 接続先の頂点とコストを格納する辺のデータ
    public struct Edge
    {
        public int To;
        public long Cost;
        public Edge(int to, long cost)
        {
            this.To = to;
            this.Cost = cost;
        }
    }
    // 頂点とその頂点までのコストを記録
    public struct P : IComparable<P>
    {
        public int A;
        public long Cost;
        public P(int a, long cost)
        {
            this.A = a;
            this.Cost = cost;
        }
        public int CompareTo(P other)
        {
            return this.Cost.CompareTo(other.Cost);
        }
    }
}

優先度付きキューに入れるのは頂点とコストの両方が必要なのでそれ用の型を用意しています。優先度はコストのみで判定 ICompareble を実装しています。

こんな感じで実装できました。

参考動画

グラフ理論⑤(ダイクストラのアルゴリズム) – YouTube

Youtubeの動画でダイクストラのアルゴリズムを解説したものがあります。プログラムはないですが、仕組みを理解するのに役立ちます。

以上。