AtCoder Beginner Contest 157 に参加した記録
AtCoder Beginner Contest 157 – AtCoder
ABC157 に参加しました。
結果はABCDの4問ACでした。事前の無事Dまで解けました。D問題よりC問題に苦戦しました。
C問題に2回WAを食らいました。
結果は パフォーマンスが1400くらいの水色、レーティングやや増でした。前回の結果と合わせて前々回の爆死分を取り戻した勘定です。このペースでいけばあと4回くらいで水色になれそうです。
では問題を振り返ります。
A – Duplex Printing
高橋君は、全 N ページから成る書類を両面印刷します。両面印刷では、1 枚の紙に 2 ページ分のデータを印刷することが出来ます。
最小で何枚の紙が必要か求めてください。
この問題はよくあるA問題ですね。2で割った値に余りがあれば1足す感じです。先に1足してから割ってもOKです。
var ans = (N + 1) / 2;
Console.WriteLine(ans);B – Bingo
3×3 のサイズのビンゴカードがあります。上から i 行目、左から j 列目の数は Ai,j です。
続けて、 N 個の数 b1,b2,⋯,bN が選ばれます。選ばれた数がビンゴカードの中にあった場合、ビンゴカードのその数に印を付けます。
N 個の数字が選ばれた時点でビンゴが達成されているか、則ち、縦・横・斜めのいずれか 1 列に並んだ 3 つの数の組であって、全てに印の付いているものが存在するかどうかを判定してください。
ビンゴゲームをシミュレートする問題です。B問題なので愚直に全部試して実行しても間に合います。たぶんB問題までは計算量は気にせず実装しても大丈夫です。
この問題ではビンゴになる候補の縦、横、斜めをすべてそろっているか確認すればいいです。
// ビンゴカード値
var A = new int[3, 3];
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
A[i, j] = sc.ReadInt();
}
}
var N = sc.ReadInt();
var B = sc.ReadIntArray(N);
var ok = false;
// 縦の判定
for (int i = 0; i < 3; i++)
{
var count = 0;
for (int j = 0; j < 3; j++)
{
foreach (var b in B)
{
if (A[i, j] == b) count++;
}
}
if (count == 3) ok = true;
}
// 横の判定
for (int i = 0; i < 3; i++)
{
var count = 0;
for (int j = 0; j < 3; j++)
{
foreach (var b in B)
{
if (A[j, i] == b) count++;
}
}
if (count == 3) ok = true;
}
// 斜めの判定2回
var countX = 0;
for (int i = 0; i < 3; i++)
{
foreach (var b in B)
{
if (A[i, i] == b) countX++;
}
if (countX == 3) ok = true;
}
countX = 0;
for (int i = 0; i < 3; i++)
{
foreach (var b in B)
{
if (A[2 - i, i] == b) countX++;
}
if (countX == 3) ok = true;
}
if (ok)
{
Console.WriteLine("Yes");
}
else
{
Console.WriteLine("No");
}もっとスマートに書けると思うんですが、コンテスト中に実装したのがこれでした。ACでればOKです。
C – Guess The Number
以下の条件を満たす 0 以上の整数が存在すれば、それらのうち最小のものを出力してください。そのような整数が存在しなければ、 -1と出力してください。
- 十進表記で丁度 N 桁である。(0 は 1 桁の整数とする。その他の整数については、先頭に 0 をつけた表記は認めない。)
- 左から数えて si 桁目は ci である。(i=1,2,⋯,M)
制約
- 入力は全て整数
- 1≤N≤3
- 0≤M≤5
- 1≤s≤N
- 0≤ci≤9
単純に矛盾する入力があれば-1にすればいいです。矛盾するのは同じ桁に異なる数字が条件になっている場合、と先頭が0になる条件の場合です。
あとは条件を満たす最小の値を出力するので、指定条件のない桁は0にすればよいです。ただし先頭桁の指定がない場合は1にしないといけません。これに気が付かずWAしました。
さらに先頭が0はだめですが 0 は許されるので、N=1 のときは 先頭が0になってもOKです。これに気が付かず2回目のWAしました。
var N = sc.ReadInt();
var M = sc.ReadInt();
var a = Enumerable.Repeat(int.MaxValue, N).ToArray();
for (int i = 0; i < M; i++)
{
var s = sc.ReadInt() - 1;
var c = sc.ReadInt();
if (a[s] == int.MaxValue || a[s] == c)
{
a[s] = c;
// 先頭が0は許されない(ただし、1桁の場合は0でもいい)
if (s == 0 && c == 0 && N != 1)
{
Console.WriteLine(-1);
return;
}
}
else
{
// 同じ桁で異なる数が指定された場合は矛盾
Console.WriteLine(-1);
return;
}
}
if (N == 1 && (a[0] == 0 || a[0] == int.MaxValue))
{
// 0の場合
Console.WriteLine(0);
return;
}
for (int i = 0; i < N; i++)
{
if (a[i] == int.MaxValue) a[i] = 0;
if (i == 0 && a[i] == 0) a[i] = 1;
Console.Write(a[i]);
}
Console.WriteLine();もうちょっときれいに書きたかったです。
D – Friend Suggestions
とあるSNSに、人 1 、人 2、 ⋯、人 N が登録しています。
この N 人の間には、 M 組の「友達関係」と、 K 組の「ブロック関係」が存在します。
i=1,2,⋯,M について、人 Ai と人 Bi は友達関係にあります。この関係は双方向的です。
i=1,2,⋯,K について、人 Ci と人 Di はブロック関係にあります。この関係は双方向的です。
以下の 4 つの条件が満たされるとき、人 a は人 b の「友達候補」であると定義します。
- a≠b である。
- 人 a と人 b はブロック関係に無い。
- 人 a と人 b は友達関係に無い。
- 1 以上 N 以下の整数から成るある数列 c0,c1,c2,⋯,cL が存在し、c0=a であり、 cL=b であり、 i=0,1,⋯,L−1 について、人 ci と人 ci+1 は友達関係にある。
人 i=1,2,…N について、友達候補の数を答えてください。
制約
- 入力は全て整数
- 2≤N≤105
- 0≤M≤105
- 0≤K≤105
- 1≤Ai,Bi≤N
- Ai≠Bi
- 1≤Ci,Di≤N
- Ci≠Di
- (Ai,Bi)≠(Aj,Bj)(i≠j)
- (Ai,Bi)≠(Bj,Aj)
- (Ci,Di)≠(Cj,Dj)(i≠j)
- (Ci,Di)≠(Dj,Cj)
- (Ai,Bi)≠(Cj,Dj)
- (Ai,Bi)≠(Dj,Cj)
一目、ややこしいです。
1 以上 N 以下の整数から成るある数列 c0,c1,c2,⋯,cL が存在し ... というところが理解しにくいですが、図にしてみるとわかりやすかったです。
入力例1の友達関係を線で結んでみると以下のような図になります。
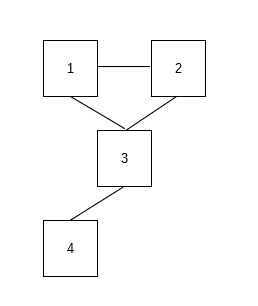
友達候補はこの図でいうと、線でつながったグループの中から、自分自身と友達関係とブロックしている人数を引いた数になります。例えばこの図の2の友達候補は、同一グループの人数が4人で、そこから自分自身と友達の2人(1, 3)を引いて1が答えになります(ブロック関係はありません)。よってこの場合2にとっては、4だけが友達候補になります。
1 以上 N 以下の整数から成るある数列 c0,c1,c2,⋯,cL が存在し、c0=a であり、 cL=b であり、 i=0,1,⋯,L−1 について、人 ci と人 ci+1 は友達関係にある。
というのが、線でつながったグループという条件で、自分自身と友達関係とブロックしている人数を引くという部分がそのほかの条件を満たすための処理です。
この図を最初に書いて思いついたのが UnionFind を使うことです。
UnionFind はグループ同士を結合することと、同一グループの判定が高速にできるデータ構造です。これを使えば上の処理をうまくできそうです。
ということで実装です。
var N = sc.ReadInt();
var M = sc.ReadInt();
var K = sc.ReadInt();
var uf = new UnionFind(N);
var frend = new List<int>[N];
var block = new List<int>[N];
for (int i = 0; i < N; i++)
{
frend[i] = new List<int>();
block[i] = new List<int>();
}
// 友達関係
for (int i = 0; i < M; i++)
{
var a = sc.ReadInt() - 1;
var b = sc.ReadInt() - 1;
frend[a].Add(b);
frend[b].Add(a);
uf.Union(a, b);
}
// ブロック関係
for (int i = 0; i < K; i++)
{
var c = sc.ReadInt() - 1;
var d = sc.ReadInt() - 1;
block[c].Add(d);
block[d].Add(c);
}
for (int i = 0; i < N; i++)
{
if (i > 0) Console.Write(' ');
// 同一グループのサイズから友達関係の数と自分自身の1を引く
var ans = uf.Size(i) - frend[i].Count - 1;
// 同一グループ内のブロック関係の数を引く
foreach (var b in block[i])
{
if (uf.Same(i, b)) ans--;
}
Console.Write(ans);
}
Console.WriteLine();UnionFind の実装は以下のページにあります。
[C#] Union-Find木を実装する方法 │ Web備忘録
備えあれば憂いなしです。
C問題と同じくらいの時間で解けました。
E問題は平衡二分探索木を使う問題だったみたいです。前に一度実装したのにどこかになくしてしまったのでもう一度実装しておこうと思いました。
以上。





コメントを書く