[C#] ワーシャルフロイドのアルゴリズムに入門する。

ワーシャルフロイドのアルゴリズムについてまとめ、C#で実装してみる記事です。

ワーシャル–フロイド法 とは

• ワーシャル–フロイド法 – Wikipedia

ワーシャル–フロイド法（英: Warshall–Floyd Algorithm）は、重み付き有向グラフの全ペアの最短経路問題を多項式時間で解くアルゴリズムである。

ワーシャルフロイドは最短経路問題を解くときに使われるアルゴリズムの1つで、Wikipediaには上記のように書いてあります。

ワーシャルフロイドのアルゴリズムは「全点対最短経路問題」を解くことができます。つまりグラフ上のすべての頂点間の最短経路を探すアルゴリズムです。計算量は O(V³) です。ここで V は頂点(vertex)の数を意味します。

V³ なので、非常に重たい計算を行うアルゴリズムなので、入力データの数によっては計算に時間がかかります。AtCoder のような競技プログラミングで使う場合は10³もあればTLEしてしまいます。

最短経路問題と聞くとややこしそう感じがしますが、このアルゴリズムの実装は非常にシンプルです。が、その反面シンプルすぎて理解しにくいところもあります。

実装例

次のようなグラフについて、各頂点間での最短経路を考えます。

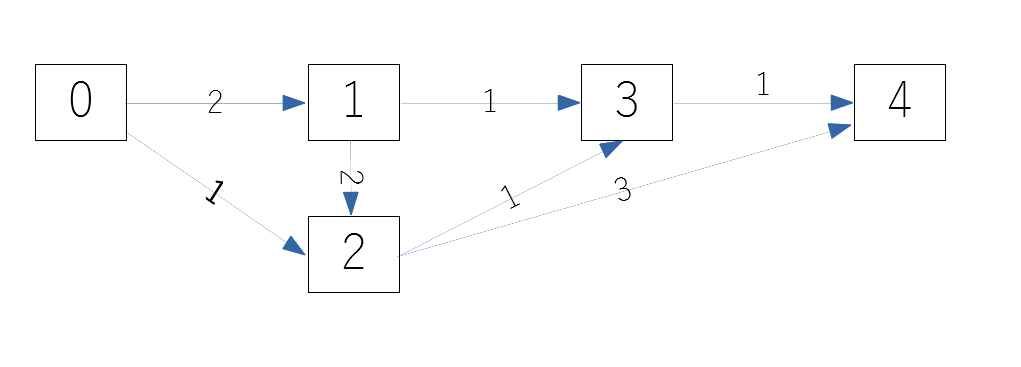
ワーシャルフロイドでは次のような3重のループで各頂点間の最短距離を求めます。

// 頂点iからjへ距離と、i->k->jとkを経由する距離を比べる
for (int k = 0; k < 5; k++)
{
    for (int i = 0; i < 5; i++)
    {
        for (int j = 0; j < 5; j++)
        {
            dp[i, j] = Math.Min(dp[i, j], dp[i, k] + dp[k, j]);
        }
    }
}

各辺のコストをDPに入れておき、辺の存在しない頂点間の距離は巨大な値(INF)を入れておきます。あとは3重のループでi, jの頂点間の距離と、kを経由する場合の距離を比較して小さいほうの値で更新していきます。

これですべての点の間の最短距離が得られます。とてもシンプルです。なお、そもそもつながる辺が存在せず到達できない場合はINFになります。

すべてのコードを載せると以下のようになります。

static void Main(string[] args)
{
    Solve(0, 4); // 3
    Solve(0, 3); // 2
    Solve(1, 2); // 2
    Solve(1, 3); // 1
    Solve(1, 4); // 2
}

static void Solve(int start, int goal)
{
    // 各辺の入力データ
    var edges = new List<Edge>();
    edges.Add(new Edge(0, 1, 2));
    edges.Add(new Edge(0, 2, 1));
    edges.Add(new Edge(1, 3, 1));
    edges.Add(new Edge(1, 2, 2));
    edges.Add(new Edge(2, 3, 1));
    edges.Add(new Edge(2, 4, 3));
    edges.Add(new Edge(3, 4, 1));

    // 頂点iからjへの最短距離を格納するDP
    // 初期値は大きな値(INF)を入れておく
    // 同じ頂点への距離は0にする
    var INF = 100000000;
    var dp = new int[5, 5];
    for (int i = 0; i < 5; i++)
    {
        for (int j = 0; j < 5; j++)
        {
            dp[i, j] = INF;
        }
        dp[i, i] = 0;
    }

    // 1つの辺で直接つながるときの距離
    foreach (var e in edges)
    {
        dp[e.From, e.To] = e.Cost;
    }

    // 頂点iからjへ距離と、i->k->jとkを経由する距離を比べる
    for (int k = 0; k < 5; k++)
    {
        for (int i = 0; i < 5; i++)
        {
            for (int j = 0; j < 5; j++)
            {
                dp[i, j] = Math.Min(dp[i, j], dp[i, k] + dp[k, j]);
            }
        }
    }

    // dp の中に頂点間の距離が格納されている
    // INFの場合は点を結ぶ辺が存在しない、到達できない
    var ans = dp[start, goal];
    Console.WriteLine(ans);
}

struct Edge
{
    public int From { get; set; }
    public int To { get; set; }
    public int Cost { get; set; }
    public Edge(int f, int t, int c)
    {
        this.From = f;
        this.To = t;
        this.Cost = c;
    }
}

INFを int.MaxValue とかにすると足し算でオーバーフローして計算が狂うので注意してください。

3重ループが入れ子になる順番に注意してください。kが経由する頂点で、一番外側に来ます。

最短経路が求まる理由

結局すべての頂点の間で、ほかの点を中継地点として選んだ時の最小の距離を求めています。

一目、「頂点の番号が入れ替わったらうまく求まらないのでは？」とも思いますが、どのような形で結ばれていようと、結局最終的には i->k と k->j は求まっているのでこれを使ってうまく最短経路が求まります。

0 -> 3 -> 2 -> 1

話を分かりやすくするために、このようなグラフを考えます。数字は頂点の番号です。各辺のコストは1とします。この時0から1への最短経路がなぜ求まるかを考えます。

var N = 4;
for (int k = 0; k < N; k++)
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            DP[i, j] = Math.Min(DP[i, j], DP[i, k] + DP[k, j]);
        }
    }
}

このループはワーシャルフロイドの最重要箇所のコードです。DPにはすでに入力が初期値として入っているものとします。

kが中継地点として考える頂点です。0と1は中継地点とはならないのでとりあえずここでは無視します。

k=2のループで 3から1 の最短経路が確定します。そして最後のk=3のループで 0から3 と 3から1 の経路がすでに求まっているので3を経由する最短経路として、0から1 の最短経路が確定します。

こんな感じで、どのような場合でも最終的に、開始地点から中継地点まで(i->k)の距離と、中継地点から目的地点まで(k->j)の距離が求まり、すべての頂点間で最短経路が確定します。

実装は簡単なので、計算量だけ気にしておけばとても使えるアルゴリズムです。

使用例

よくわからないので実際に実装して問題を解いてみようと思います。

AtCoder の問題をワーシャルフロイドで解いて、正しく実装できるか確認してみます。

D: Wall – AtCoder Beginner Contest 079 | AtCoder

解くのは上の問題です。

一見グラフ問題に見えないのですが、ある数を別の数に変換するときのコストを全パターンワーシャルフロイドのアルゴリズムを使って前計算しておくことで効率的に答えが求まります。

// 入力省略
var dp = new int[10, 10];
for (int i = 0; i < 10; i++)
{
    for (int j = 0; j < 10; j++)
    {
        dp[i, j] = C[i, j];
    }
}
for (int k = 0; k < 10; k++)
{
    for (int i = 0; i < 10; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            dp[i, j] = Math.Min(dp[i, j], dp[i, k] + dp[k, j]);
        }
    }
}

var ans = 0;
for (int i = 0; i < H; i++)
{
    for (int j = 0; j < W; j++)
    {
        if (A[i, j] == -1) continue;
        ans += dp[A[i, j], 1];
    }
}
Console.WriteLine(ans);

ACできたのでうまく実装できてました。

以上。