[C#] セグメント木を実装してみる │ Web備忘録

1. セグメント木とは
- 1.1. なにができるのか
2. セグメント木の仕組み
3. C# での実装
4. 実装を確認する
5. 参考URL

セグメント木とは

セグメント木は名前の通り区間を扱うのが得意なデータ構造です。中身は完全二分木であり、区間の持つデータを管理します。

要素8件からなる配列のデータについて、セグメント木は具体的には以下のような形になります。

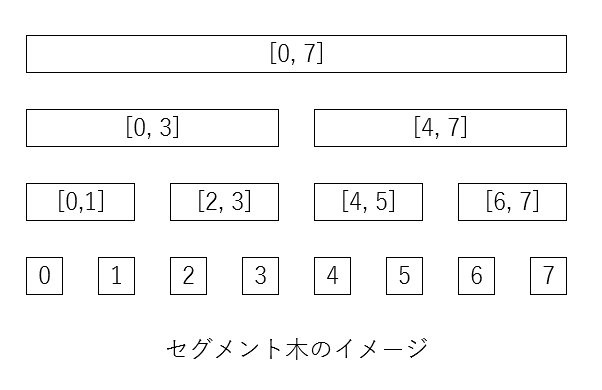
各ノードの中の数字は配列の区間データを格納します。

上記のような二分木のデータ構造を使うと、区間に関するクエリ(データの更新、取得)を計算量 O(log N)行えます。

なにができるのか

セグメント木は各節にどのようなデータを持たせるかによって様々な機能を実現できます。代表的なのが区間の最小値を求める機能　Range Minimum Query (RMQ)です。

例えば [2 3 1 4] というようなデータがあったとき、指定した区間の中から最小値を取得できます。例えば区間1から3の範囲 [1, 4) の最小値は 1 です。これを O(log N) で求められます。

また、区間の1点を更新することができます。データを更新すると、セグメント木のデータも再計算する必要がありますが、これも O(log N) で実現できます。

以下、区間最小値を求めるセグメント木を考えていきます。

セグメント木の仕組み

構成

セグメント木は配列のデータから区間に関するクエリを実行します。セグメント木は完全二分木で実際の配列データと、区間データを管理します。

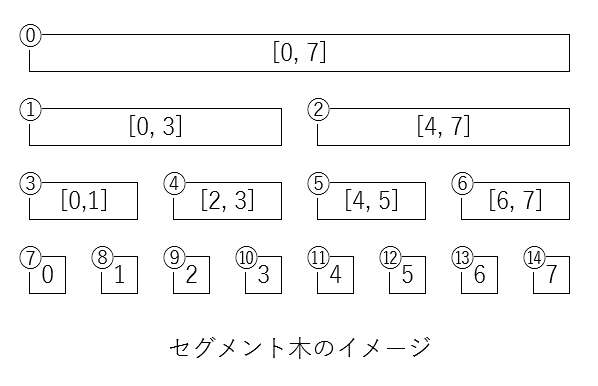
セグメント木のデータは内部的には配列で管理できます。中にはそれぞれが対応する区間の最小値を格納します。上記画像の左上の数字がセグメント木内部の配列のインデックスを意味します。

セグメント木は葉に n 個の要素を持ちます。この葉部分のデータが元の配列データが格納されている部分になります。

なお、nが2のべき乗ではない場合、いい感じのデータで埋めて使います。例えば区間の最小値を求める場合にはINFを入れておくような感じです。とりあえずデータ数を2のべき乗として進めます。

また、セグメント木はデータ数をnとすると 2ⁿ-1 個のノードからなる完全二分木となります。あるノードは子ノードの対応する区間を合わせた区間のデータを管理しています。

例として 2 1 3 1 2 3 3 1 という配列の区間最小値を求めるセグメント木は、以下のようにデータを保持します。

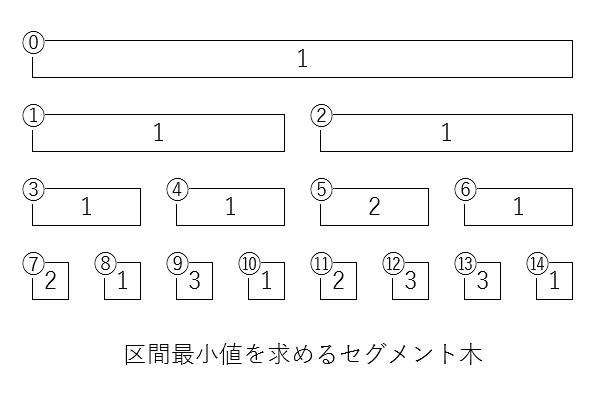
ノードの中の数字は対応する区間の最小値(子ノードの持つデータの最小値)を保持することになります。

データの更新

セグメント木が管理するデータはわかりました。次にデータの更新を考えます。

例えば配列内のある1件のデータを更新することを考えます。

まずそのインデックスが対応するセグメント木のノード(葉)を更新する必要があります。

次に更新したノードの親ノードを再帰的に更新することで、そのノードが対応する区間すべての最小値を更新できます。この時、葉からルートまでたどるので計算量が O(log N) となります。

更新した葉ノードのインデックスを x とすると (x-1)/2 で親のノードが求まります。

これでデータの更新はうまくいきました。

例えば、2 1 3 1 2 3 3 1 という配列a について、a[5]=0 に更新した時のセグメント木の更新イメージ図が以下のようになります。

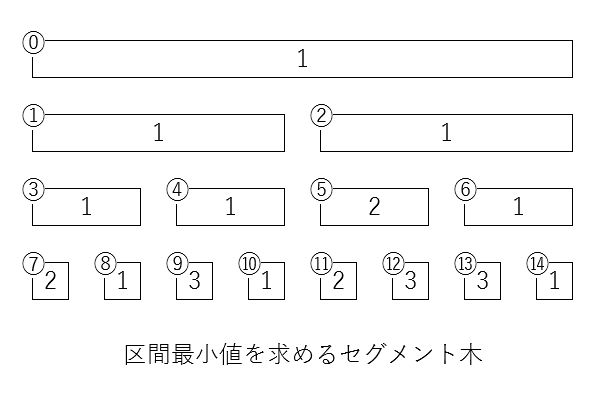
↑のようなデータから更新されて、

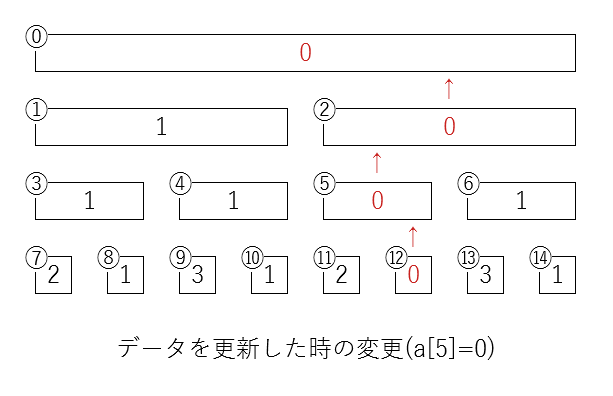
こんな感じで更新が行はれます。

葉から順番に最小値が更新されているようなイメージです。

区間データの取得

データの更新ができるようになったので、区間最小値を求める方法を考えます。

区間の取得は更新とは逆で、ルートノードから再帰的に対応区間を探していきます。答えの返せるノードの場合は答えを返し、そうでない場合は子ノードを再帰的に評価して答えを取得します。評価のパターンは以下のいずれかになります。

現在のノードの対応区間が、求める区間に含まれない場合 -> INFを返す。
- 例) [6, 8) が現在のノードの対応区間で、[1, 5) の区間最小値を求めるとき。
現在のノードの対応区間が、求める区間に完全に含まれる場合 -> 現在のノードの値を返す。
- 例) [2, 4) が現在のノードの対応区間で、[1, 5) の区間最小値を求めるとき。
上記以外の場合、現在のノードの対応区間が、求める区間を一部を含む場合 -> 2つの子ノードを再帰的に評価し、最小値を返す。
- 例) [0, 8) が現在のノードの対応区間で、[1, 5) の区間最小値を求めるとき。
- 例) [4, 6) が現在のノードの対応区間で、[1, 5) の区間最小値を求めるとき。

1 の場合、求めたい区間に含まれないのでそもそも答えに関係がありません。したがって答えに影響しないような値を返します。区間最小値を求める場合は大きな値(INF)を返しておきましょう。

2 の場合、求めたい区間に現在のノードの対応区間が完全に含まれる場合は、これを答え(最小値)の候補にしてよいため、ノードの持つ値をそのまま返せばよいです。

3 の場合、求めたい区間が部分的に含まれていますが、含まれていない区間の値が最小値となっている場合もあるため、このノードの値は使えません。2つの子ノードを再帰的に評価する必要があります。

上記手順でルートから再帰的に対応する区間のデータを取得すると答えが求まります。ルートから子ノードをたどっていくので、計算量は O(log N) になります。

実装上は半開区間で考えたほうがよいので、以下半開区間でのイメージを載せておきます。

2 1 3 1 2 3 3 1 のデータから区間 [1, 5) の最小値を求めるとき、以下のように再帰的にノードをたどります。

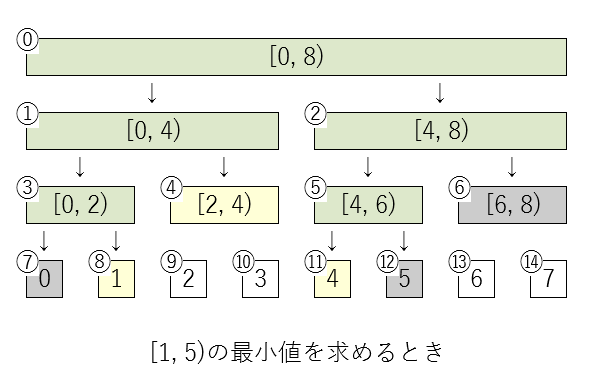
グレー背景が 1 のパターンで、黄色が 2 のパターン、緑が 3 のパターンです。

まずルートから初めて [0, 8) は一部を含むので子ノードを評価します。同様に [0, 4) [0, 2) とたどります。葉も同じように考えて、0は含まないのでINFを返し、1は含まれるのでその値を返します。

[2, 4) は求めたい区間に含まれるためノードを値をそのまま使えます。

こんな感じで区間の値が求まるようになります。

C# での実装

C#で実装してみます。

class SegmentTree
{
    // 元の配列の大きさ
    public int N { get; set; }
    // セグメント木のデータ(2^n-1)
    public int[] Node { get; set; }

    // 元データの配列を引数で渡す
    public SegmentTree(int[] a)
    {
        // 要素数を2のべき乗とする
        N = 1;
        while (N < a.Length) N *= 2;

        // セグメント木の管理する要素数を 2^n-1 で初期化する
        this.Node = new int[2 * N - 1];
        for (int i = 0; i < this.Node.Length; i++) this.Node[i] = INF;

        // 各ノードの値を初期化する
        // 葉は元の配列のデータ
        for (int i = 0; i < a.Length; i++) this.Node[N + i - 1] = a[i];
        // 子ノードを比較して親ノードの値を決めていく
        for (int i = N - 2; i >= 0; i--)
        {
            this.Node[i] = this.Compare(this.Node[2 * i + 1], this.Node[2 * i + 2]);
        }
    }

    // x番目のデータをvに更新する
    public void Update(int x, int v)
    {
        // 元の配列のデータが格納される葉のデータを更新する
        x += (this.N - 1);
        this.Node[x] = v;

        // 更新したノードの親をさかのぼってルートまで更新する
        while (x > 0)
        {
            // 親ノードのインデックス
            x = (x - 1) / 2;
            this.Node[x] = this.Compare(this.Node[2 * x + 1], this.Node[2 * x + 2]);
        }
    }
    // [a, b) の区間最小値を求める
    public int GetMin(int a, int b)
    {
        return this.GetMin(a, b, 0, 0, this.N);
    }
    // [a, b) の区間最小値を求める
    // 現在のノードはk番目、[l, r)
    private int GetMin(int a, int b, int k, int l, int r)
    {
        // 1. 現在のノードの対応区間が、求める区間に含まれない場合
        //    対象外の区間のデータなので、最小値に関係のない値(INF)を返す
        if (r <= a || b <= l) return INF;

        // 2. 現在のノードの対応区間が、求める区間に完全に含まれる場合
        //    現在のノードの値が最小値の候補になるのでそのまま返す
        if (a <= l && r <= b) return this.Node[k];

        // 3. 上記以外の場合、現在のノードの対応区間が、求める区間を一部を含む場合
        //    子ノードを評価し、比較した結果を返す
        var vl = this.GetMin(a, b, 2 * k + 1, l, (l + r) / 2);
        var vr = this.GetMin(a, b, 2 * k + 2, (l + r) / 2, r);
        return this.Compare(vl, vr);
    }

    // 2要素を比較して小さい値を返す
    private int Compare(int a, int b) { return Math.Min(a, b); }
}
public static int INF = int.MaxValue;

GetMin() が区間最小値を求める関数で、Update() が1件のデータを更新する関数です。

それぞれ見ていきます。

構成する

区間データを求めたい配列データを用意します。これを使ってコンストラクタ内でセグメント木の内部データを構築します。

データ数が2のべき乗になるように考えます。例えばデータ数が 5 の場合は 8 にします。足りないデータは INF を入れておきます。こうすると最小値には影響ありません。

次に葉の値を埋めます。これは簡単です。

その後、葉以外のノードを後ろから埋めていきます。子ノードの値を比較して最小値を格納します。子ノードのインデックスは 2*x + 1 と 2*x + 2 になります。

// 元データの配列を引数で渡す
public SegmentTree(int[] a)
{
    // 要素数を2のべき乗とする
    N = 1;
    while (N < a.Length) N *= 2;

    // セグメント木の管理する要素数を 2^n-1 で初期化する
    this.Node = new int[2 * N - 1];
    for (int i = 0; i < this.Node.Length; i++) this.Node[i] = INF;

    // 各ノードの値を初期化する
    // 葉は元の配列のデータ
    for (int i = 0; i < a.Length; i++) this.Node[N + i - 1] = a[i];
    // 子ノードを比較して親ノードの値を決めていく
    for (int i = N - 2; i >= 0; i--)
    {
        this.Node[i] = this.Compare(this.Node[2 * i + 1], this.Node[2 * i + 2]);
    }
}

データの更新

// x番目のデータをvに更新する
public void Update(int x, int v)
{
    // 元の配列のデータが格納される葉のデータを更新する
    x += (this.N - 1);
    this.Node[x] = v;

    // 更新したノードの親をさかのぼってルートまで更新する
    while (x > 0)
    {
        // 親ノードのインデックス
        x = (x - 1) / 2;
        this.Node[x] = this.Compare(this.Node[2 * x + 1], this.Node[2 * x + 2]);
    }
}

データを更新するのは簡単です。対応する葉の値を更新し、親をたどりながら更新しています。

区間データの取得

// [a, b) の区間最小値を求める
public int GetMin(int a, int b)
{
    return this.GetMin(a, b, 0, 0, this.N);
}
// [a, b) の区間最小値を求める
// 現在のノードはk番目、[l, r)
private int GetMin(int a, int b, int k, int l, int r)
{
    // 1. 現在のノードの対応区間が、求める区間に含まれない場合
    //    対象外の区間のデータなので、最小値に関係のない値(INF)を返す
    if (r <= a || b <= l) return INF;

    // 2. 現在のノードの対応区間が、求める区間に完全に含まれる場合
    //    現在のノードの値が最小値の候補になるのでそのまま返す
    if (a <= l && r <= b) return this.Node[k];

    // 3. 上記以外の場合、現在のノードの対応区間が、求める区間を一部を含む場合
    //    子ノードを評価し、比較した結果を返す
    var vl = this.GetMin(a, b, 2 * k + 1, l, (l + r) / 2);
    var vr = this.GetMin(a, b, 2 * k + 2, (l + r) / 2, r);
    return this.Compare(vl, vr);
}

[l, r) が現在のノードの区間です。[a, b) が求めたい区間です。両方ともに半開区間なのを注意します。

k が現在のノードのインデックスです。

半開区間でおいたので、子ノードが対応する区間が [l, (l+r)/2) と [(l+r)/2, r) になります。あとは子ノードのインデックスがわかれば呼び出せます。

実装を確認する

judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=DSL_2_A&lang=jp

AOJ に Range Minimum Query (RMQ) という区間最小値を求める問題があるのでこれで動作を確認できます。

以上。

参考URL

[NodeJS] log4js でログをいい感じに出力する方法

AtCoder Beginner Contest 153 に参加した記録

[C#] セグメント木を実装してみる

セグメント木とは

なにができるのか

セグメント木の仕組み

構成

データの更新

区間データの取得

C# での実装

構成する

データの更新

区間データの取得

実装を確認する

参考URL

C#カテゴリの最新記事

名前付きキャプチャで記録した内容を複数個所でマッチさせる正規表現 [C#]

[C#] リストやコレクションを辞書にやセット変換する方法 [ToDictionary][ToHashSet]

[WPF,Prism] ダイアログ表示をDialogServiceで行う方法 [C#]

[WPF,Prism] RegionManagerによる画面遷移方法まとめ

[C#] 名前空間内の型(クラス)をリフレクションで列挙する方法

[C#] トースト通知とリマインダを実装する方法