[C#] モンテカルロ法で円周率πを求める

モンテカルロ法とは

モンテカルロ法 とは、乱数を使っていろいろ計算してみよう、みたいなことです。詳しくはWikipediaをご覧下さい。

モンテカルロ法のアルゴリズムを使って、円周率πを計算してみます。

円周率πのを求める考え方

1. 1辺が1の正方形を用意します。
2. そこに半径1の円の1/4を書きます。
3. 正方形の内側にランダムに1点選び、円の内側かどうかを判定します。
4. 3の処理をn回繰り返します。
5. 円の内側の点の数 / n ≒ π / 4 となります。(点の数は面積に比例するため)

5でなぜ、π/4にほぼ等しくなるかというと、まず正方形の面積は1²です。 円の面積がπr
²、したがってその1/4(r=1)なので、円の内側の面積はπ/4となります。 したがって、

円の内側の点の数 / n ≒ π / 4

となります。

モンテカルロ法のプログラム

上記の考え方を元に、円周率をプログラムで求めてみます。 試行回数を1000回とし、0から1の間で生成される乱数の組(x, y)が円の内側かどうかを判定します。 判定には以下の条件式を使用します。

x² + y² <= 1

底辺x、高さyの三角形の斜辺を三平方の定理で求め、それが1(半径)寄り小さいと円の内側と判定できます。

以下の図はWikipediaをからの引用です。イメージがつかめると思います。

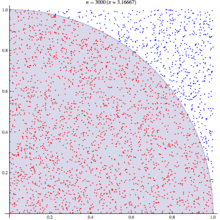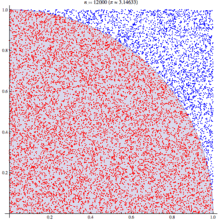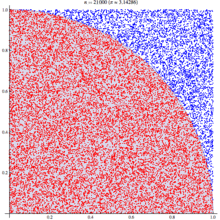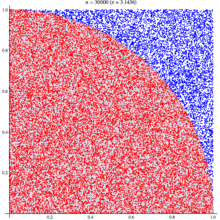
実装例

public static int Seed = Environment.TickCount;
public static double MontePi(int n)
{
    var rand = new Random(Seed++);
    var count = 0;
    if (n < 1) return 0;
    for (int i = 0; i < n; i++)
    {
        var x = rand.NextDouble();
        var y = rand.NextDouble();
        if (x * x + y * y <= 1)
        {
            count++;
        }
    }
    return 4.0 * count / n;
}

試行回数nを引数として渡すと、円周率πの近似値を返す関数です。

実行結果

試行回数(引数n)が大きくなればなるほど精度は高くなりますが、乱数に偏りがあれば精度は低くなります。

試しに100000000を引数にして10回実行してみました。

• 3.1414248
• 3.1416244
• 3.141972
• 3.1414728
• 3.14234
• 3.1428124
• 3.1407884
• 3.1411048
• 3.1412912
• 3.1413948

ほぼ3.141くらいまでは近似しているのが確認できました。
ちなみに1億を引数にすると、1回の処理で数秒かかりますが3.141までは10件とも求ました。