Judge System Update Test Contest 202004
Judge System Update Test Contest 202004 – AtCoder
AtCoderのジャッジ環境更新負荷テストのコンテストに参加したので記録しておきます。
今回のコンテストはジャッジ環境更新に伴う負荷テストが目的のため Unrated です。成功しても失敗してもレートは変動しないため気楽に参加できました。
ジャッジシステムの更新に伴いコンテストで使用できる言語に大きな変更があります。このコンテストでは旧環境で使えていた言語バージョンが使えなくなっており、新しいバージョンが使えるようになっています。
C# のジャッジ環境変更点
例として、私の使っているC#の場合だと C#(Mono 4.6.2.0) しか使えなかったのが、
- .NET Core 3.1.201
- Mono-mcs 6.8.0.105
- Mono-csc 3.5.0
の3バージョンが使えるようになっています。今後はこの中の .NET Core 3.1 のC#を使って参加することになりそうです。
旧環境だとC#6.0相当の機能しかおそらく使えなかったと思いますが、C#8.0まではたぶん対応しているんだと思います。とはいえ競技プログラミングに役立つ機能があるかと言われれば微妙で、タプルのリテラルが書きやすくなった程度だと思います。
// 旧環境ではこう書いていたのが
var tup1 = Tuple.Create(1, 2, 3);
// 新環境だとこう書ける
var tup2 = (1, 2, 3);
// 変数のスワップもかける
var a = 1;
var b = 2;
(b, a) = (a, b);タイプ量が減るのでコードの見通しはよくなると思います。例えば Queue を使ってBFSとかする時にタプルを書くのが面倒だったのがなくなるなどは考えられます。
一応、古い書き方のタプルと新しいタプルは共存できるようなのでライブラリはしばらく使いまわせそうです。
コンテストの振り返り。
普段のABCと違いD問題までの4問でした。難易度は普段のABCのD問題までとあまり変わりありません。
めちゃくちゃしょうもないバグを書いてWAしましたが4問全完しました。
振り返ります。
A – Walking Takahashi
数直線上で生活している高橋君は、いま座標 S にいます。座標が L 以上 R 以下の区間は日当たりが良いです。
日に当たりたい高橋君は座標が L 以上 R 以下になるまで次のような移動を繰り返します。
- 現在の座標を X として、L≤X≤R のとき移動をやめる。X が L 未満のとき、X+1 に移動する。
X が R より大きいとき、X−1 に移動する。
高橋君が最終的に移動をやめる座標を求めてください。
SがLより小さければLに、Rより大きければRに移動するのが答えになります。それ以外はSのまま移動しません。
var S = sc.ReadInt();
var L = sc.ReadInt();
var R = sc.ReadInt();
if (L <= S && S <= R)
{
Console.WriteLine(S);
}
else if (S < L)
{
Console.WriteLine(L);
}
else
{
Console.WriteLine(R);
}B – Picking Balls
赤か青で塗られた N 個のボールが入った袋があります。また、それぞれのボールには整数が書かれています。
i 個目のボールには整数 Xi が書かれており、色は Ci が R のとき赤、B のとき青です。
高橋君は、袋の中にボールが残っている間、次の手順を繰り返して袋からボールを取り出します。
- 袋の中に赤のボールがあるとき、残っている赤のボールのうち最小の整数が書かれたボールを袋から取り出す。そうでないとき、残っている青のボールのうち最小の整数が書かれたボールを袋から取り出す。
高橋君が各手順で取り出したボールに書かれていた整数を求めてください。
赤の小さい順、青の小さい順にソートすればよいです。C#だと linq を使ってキーを2つ指定できます。C++だとどうやってソートするのかわからないです。
あるいは赤と青で別のリストに分けてそれぞれソートして赤、青の順に出力してもよいです。
// 旧環境では Tuple<int, char>[N] としていた
var XC = new (int, char)[N];
for (int i = 0; i < N; i++)
{
var x = sc.ReadInt();
var c = sc.ReadStr()[0];
XC[i] = (x, c);
}
// 'R', 'B' に並べたいので文字の降順、数の昇順でソートして出力
foreach (var t in XC.OrderByDescending(xc => xc.Item2).ThenBy(xc => xc.Item1))
{
Console.WriteLine(t.Item1);
}せっかくなので入力の値をタプルの配列で受けてみました。特に違和感なく書けます。
C – Numbering Blocks
積み木の山が 3 つ並んでおり、それぞれの山には a1≥a2≥a3 個の積み木が積まれています。
全部で N=a1+a2+a3 個の積み木がありますが、これらに 1 から N までの整数をちょうど 1 つずつ書き込みます。
ただし、次の条件を全て満たす必要があります。
- 左から i 個目の山の下から j 個目の積み木に書かれた整数を Xi,j で表す (1≤i≤3,1≤j≤ai) とき、
- Xi,j>Xi,j−1(1≤i≤3,1<j≤ai)
- Xi,j>Xi−1,j(1<i≤3,1≤j≤ai)
この条件を満たす整数の書き込み方の個数を求めてください。
制約
- 3≥a1≥a2≥a3≥1
- 入力は全て整数である
問題だけ読むとわかりにくいですが、入力例2に画像があったので引用します。
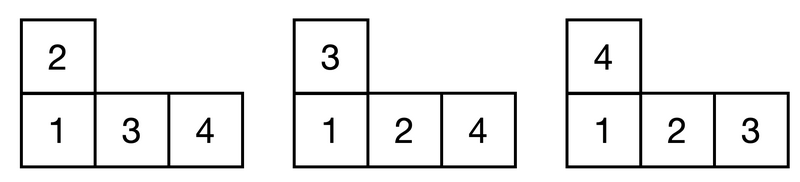
入力が 2 1 1 の時、左から2段1段1段に積み木を積みます。この時下の段の積み木は必ず上の段の積み木より小さくなければなりません。また隣り合った積み木は左のほうが小さくなければなりません。ただし2段目のように隣が積まれていない場合もあります。
実装的には積み木に書かれる数字の全パターンを列挙し、愚直に条件を満たすかどうか判定すればよいです。
積み木はすべて異なる数を書き込むので全順列を列挙すればよいです。C++でいうところの next_permutation です。今回だと最大で9!=362880 パターンしかないので全探索しても十分間に合います。
[C#] 順列を求める next_permutation() 代わりを実装する方法 │ Web備忘録
順列をC#で求めるコードは上の記事を参考にしてください。
あとはうまく列挙したパターンをXにはめ込んで判定すればよいのですが、結構手間取ってしまい20分近く実装にかかってしまいました。実装がDより難しくて焦りました。
// 全順列を生成する関数
static List<T[]> AllPermutation<T>(params T[] array) where T : IComparable
{
var a = new List<T>(array).ToArray();
var res = new List<T[]>();
res.Add(new List<T>(a).ToArray());
var n = a.Length;
var next = true;
while (next)
{
next = false;
int i;
for (i = n - 2; i >= 0; i--)
{
if (a[i].CompareTo(a[i + 1]) < 0) break;
}
if (i < 0) break;
var j = n;
do
{
j--;
} while (a[i].CompareTo(a[j]) > 0);
if (a[i].CompareTo(a[j]) < 0)
{
var tmp = a[i];
a[i] = a[j];
a[j] = tmp;
Array.Reverse(a, i + 1, n - i - 1);
res.Add(new List<T>(a).ToArray());
next = true;
}
}
return res;
}
var A = sc.ReadIntArray(3);
var sum = A.Sum();
// [1..N]
var list = Enumerable.Range(1, sum).ToArray();
// 全順列生成
var p = AllPermutation(list);
var ans = 0;
// 全パターンを試して条件を満たすものを数える
foreach (var pt in p)
{
// 頑張って判定する
var ok = true;
var index = 0;
var X = new int[3, 3];
for (int i = 0; i < A[0]; i++)
{
X[0, i] = pt[index++];
}
for (int i = 0; i < A[1]; i++)
{
X[1, i] = pt[index++];
}
for (int i = 0; i < A[2]; i++)
{
X[2, i] = pt[index++];
}
for (int i = 0; i < 3; i++)
{
var prev = 0;
for (int j = 0; j < A[i]; j++)
{
if (prev > X[i, j] && X[i, j] != 0) ok = false;
prev = X[i, j];
}
}
for (int j = 0; j < 3; j++)
{
var prev = 0;
for (int i = 0; i < 3; i++)
{
if (prev > X[i, j] && X[i, j] != 0) ok = false;
prev = X[i, j];
}
}
if (ok) ans++;
}
Console.WriteLine(ans);たぶんもっとスマートな書き方があると思います。
D – Calculating GCD
長さ N の整数列 A1,A2,⋯,AN があります。
Q 個の 1 より大きい整数 S1,S2,⋯,SQ が与えられるので、i=1,2,⋯,Q について次の問題で X=Si とした場合の答えを求めてください。
- 初め整数 X がある。j=1,2,⋯,N の順に、X を gcd(X,Aj) で置き換えるという操作を行う。j 回目の操作の直後に X=1 であるような j が存在する場合はそのような j の最小値を、存在しない場合は最終的な X の値を求めよ。
制約
- 1≤N,Q≤105
- 1≤Ai≤109
- 1<Si≤109
- 入力は全て整数である
問題文の操作を愚直にシミュレートしてしまうと計算量が O(N^2) かかってしまう問題です。こういう時はあらかじめ前計算しておいて計算量を落とすというようなことが多いです。
今回の問題だと Si と A1 .. AN を順番にGCDしていくことになりますが、GCDは順番は関係ないのであらかじめA1からANまでのGCDを計算しておけば、最終的なXの値(GCDの結果)は O(1) で求まります。
ただし今回の問題だとさらにGCDの結果が1になるような場合はどのタイミングで1になるかも求めなければいけません。ということで最終的なGCDの結果だけを前計算するのではなく、累積和のように累積GCDを管理しておく必要があります。この累積GCDの各値とSiをGCDした時に最初に1になる場所が、求めるjの最小値になります。
あるjで累積GCDとSiのGCDが1になったら以降すべて1になります。なので二分探索して最初に1になる場所を見つけましょう。そうすることで O(QlogN) で解けました。
static long Gcd(long a, long b)
{
if (b == 0) return a;
return Gcd(b, a % b);
}
var N = sc.ReadInt();
var Q = sc.ReadInt();
var A = sc.ReadLongArray(N);
var S = sc.ReadLongArray(Q);
// 累積GCDを求めておく
var gcd = A[0];
var sumg = new long[N + 1];
for (int i = 0; i < N; i++)
{
var a = A[i];
gcd = Gcd(gcd, a);
sumg[i + 1] = gcd;
}
foreach (var s in S)
{
// 最終的なGCDが1以外の場合
var g = Gcd(s, gcd);
if (g != 1)
{
Console.WriteLine(g);
continue;
}
// 最初にGCDが1になる場所を二分探索
var l = 0;
var r = N;
while (r - l > 1)
{
var mid = l + (r - l) / 2;
var next = Gcd(sumg[mid], s);
if (next == 1) r = mid;
else l = mid;
}
Console.WriteLine(r);
}インライン関数が使えるようになっているので、上のコードをメイン関数に貼り付けても動くようになりました。インライン関数が使えるのは便利かもしれません。いちいち入力をstaticに書いたりをしなくてもうまく動かせるかもしれません。
累積和的要素+二分探索+GCDみたいな合わせ技の問題でした。
この問題は var mid = l + (r - 1) / 2; としょうもないバグで無駄なTLEをやらかしました。よく見ると l+(r-1) となっていて、l と 1 をタイプミスしてました。見やすいフォントに変えようと思いました。
以上。





コメントを書く