ABC035 D – トレジャーハント を解く
D: トレジャーハント – AtCoder Beginner Contest 035 | AtCoder
ABC035 D – トレジャーハント を C# を使って解いてみます。
この問題は AtCoder Beginner Contest 035 の D問題で、最短経路を求める問題です。問題は以下のようになっています。
高橋君が住む国には N 箇所の町と町同士をつなぐ一方通行の道が M 本あり、それぞれの町には 1 から N の番号が割りふられています。 i 番目の道は ai 番の町から bi 番の町へ移動することが可能であり、移動に ci 分だけかかります。
所持金が 0 円の高橋君は T 分間のトレジャーハントに出かけることにしました。高橋君は開始 0 分の時点で 1 番の町にいます。また、開始から T 分の時点にも 1 番の町にいなくてはなりません。高橋君が i 番の町に 1 分間滞在すると、 Ai 円が高橋君の所持金に加算されます。
T 分間のトレジャーハントによって高橋君の所持金は最大いくらになるか求めてください。
入力と制約
- 1 行目に町の数と道の数、トレジャーハントの分数を表す 3 つの整数 N,M,T(2≦N≦105,1≦M≦min(N(N−1),105),1≦T≦109) が空白区切りで与えられる。
- 2 行目には i 番目の町に滞在したときに得られるお金の情報を表す整数 Ai(1≦Ai≦105) が空白区切りで与えられる。
- 3 行目から続く M 行のうち i 行目においては、 i 番目の道の情報を表す 3 つの整数 ai,bi,ci(1≦ai,bi≦N,ai≠bi,1≦ci≦105)が空白区>切りで与えられる。
- i≠j であるような i,j において、ai≠aj または bi≠bj のどちらかが成立する。
考え方
グラフ上の頂点に滞在することでお金がもらえるというお話です。
まず複数の頂点に滞在する必要はありません。より所持金の増える頂点に長く滞在したほうがより良いからです。つまり、滞在する頂点が決まればそこに最短経路で進み、滞在を終えると最短経路で戻る必要があります。
したがって、すべての頂点vについて、1番目の頂点からvを経由して1番目に戻る最短経路が高速に求まれば、トレジャーハントができるT分から移動にかかる時間を引いた残りの時間を滞在する時間にできるので、最終的な所持金の最大が求まります。
こんなイメージです。
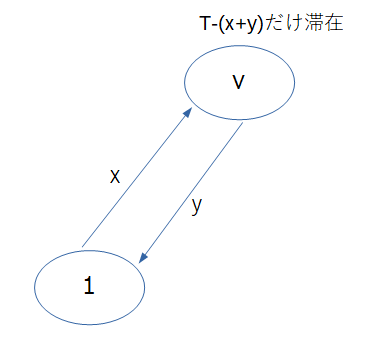
頂点1からvまでの最短経路をx, vから1までの最短経路をyとすると、T-(x+y) だけ滞在できるのでこれに A[v] をかけた値が最終的な所持金となります。これの最大がこの問題の答えです。
もちろん到達できない頂点や、到達できるが戻ってこれない頂点もあり得ます。ただし、1番目の頂点から移動せずに滞在し続けることもできるので、答えは必ず求まります。
vから1への最短経路
さて、上記の通り解く方針を立てましたが、問題は頂点vから1への最短経路の求め方です。
頂点1からvへの最短経路はダイクストラ法を使って求まります。ダイクストラ法は単一始点からすべての頂点への最短経路を求めることができるアルゴリズムなので、頂点1を始点としてダイクストラ法を用いるとvへの最短経路が求まります。
しかし頂点vから1は難しいです。すべての頂点から1までの最短経路を単純に求めると、ダイクストラ法をN回行うことになりTLEになります。また、ワーシャルフロイドのアルゴリズムで全点間の最短経路を求める方法もありますが、これは計算量が O(N3) かかりとても間に合いません。したがって以下のような工夫を行います。
今回与えられるグラフは有向グラフですが、辺の向きがすべて逆向きのグラフを考えます。こうすると何がうれしいかというと、vから1への最短経路を求める問題が、逆向きに辺を張ったグラフについて、1からvへの最短経路を求める問題に置き換わります。これはダイクストラ法で高速に求まります。
こうなると話は簡単で、ダイクストラ法を2回行うだけですべての頂点vについての 1 -> v -> 1 という移動経路の最短経路が求まります。vに向かう最短経路がダイクストラ法、vから1に帰る最短経路が逆向きに辺を張ったグラフのダイクストラ法で求まりました。
実装
static void Solve()
{
// 入力
var N = sc.ReadInt();
var M = sc.ReadInt();
var T = sc.ReadLong();
var A = sc.ReadLongArray(N);
// 通常のグラフと逆向きのグラフを考える
var dij = new Dijkstra(N);
var dijR = new Dijkstra(N);
for (int i = 0; i < M; i++)
{
var a = sc.ReadInt() - 1;
var b = sc.ReadInt() - 1;
var c = sc.ReadLong();
dij.Add(a, b, c);
dijR.Add(b, a, c);
}
// 通常のグラフの頂点0からの最短経路
var dist = dij.Calc(0);
// 逆向きのグラフの頂点0からの最短経路
var distR = dijR.Calc(0);
// 最終的な所持金を最大化する
var ans = A[0] * T;
for (int i = 1; i < N; i++)
{
if (dist[i] == Dijkstra.INF || distR[i] == Dijkstra.INF) continue;
var cost = dist[i] + distR[i];
var waitTime = T - cost;
var res = waitTime * A[i];
ans = Math.Max(ans, res);
}
Console.WriteLine(ans);
}
// ダイクストラ
class Dijkstra
{
public const long INF = long.MaxValue / 2;
public int V { get; set; }
public int E { get; set; }
public List<Edge>[] G { get; set; }
public Dijkstra(int n)
{
this.V = n;
this.G = new List<Edge>[V];
for (int i = 0; i < V; i++)
{
this.G[i] = new List<Edge>();
}
}
public void Add(int a, int b, long cost = 1)
{
this.G[a].Add(new Edge(b, cost));
this.E++;
}
public long GetMinCost(int start, int goal)
{
var cost = new long[V];
for (int i = 0; i < V; i++) cost[i] = INF;
cost[start] = 0;
var capacity = Math.Max(1, E);
var q = new PriorityQueue<P>(false);
q.Enqueue(new P(start, 0));
while (q.Count > 0)
{
var p = q.Dequeue();
if (p.Cost != cost[p.A]) continue;
foreach (var e in this.G[p.A])
{
if (cost[e.To] > p.Cost + e.Cost)
{
cost[e.To] = p.Cost + e.Cost;
q.Enqueue(new P(e.To, cost[e.To]));
}
}
}
return cost[goal] == long.MaxValue ? -1 : cost[goal];
}
public long[] Calc(int start)
{
var visited = new bool[V];
var cost = new long[V];
for (int i = 0; i < V; i++) cost[i] = INF;
cost[start] = 0;
var capacity = Math.Max(1, E);
var q = new PriorityQueue<P>(false);
q.Enqueue(new P(start, 0));
while (q.Count > 0)
{
var p = q.Dequeue();
visited[p.A] = true;
if (p.Cost != cost[p.A]) continue;
foreach (var e in this.G[p.A])
{
if (cost[e.To] > p.Cost + e.Cost && !visited[e.To])
{
cost[e.To] = p.Cost + e.Cost;
q.Enqueue(new P(e.To, cost[e.To]));
}
}
}
return cost;
}
public struct Edge
{
public int To;
public long Cost;
public Edge(int to, long cost)
{
this.To = to;
this.Cost = cost;
}
}
public struct P : IComparable<P>
{
public int A;
public long Cost;
public P(int a, long cost)
{
this.A = a;
this.Cost = cost;
}
public int CompareTo(P other)
{
return this.Cost.CompareTo(other.Cost);
}
}
class PriorityQueue<T>
{
public int Count;
private int Capacity;
private bool IsMaxHeap;
private T[] Buffer;
private IComparer<T> Cmp;
public PriorityQueue(bool isMaxHeap = true, IComparer<T> cmp = null)
{
Count = 0;
Capacity = 1 << 10;
IsMaxHeap = isMaxHeap;
Buffer = new T[Capacity];
if (cmp != null) Cmp = cmp;
else Cmp = Comparer<T>.Default;
}
public PriorityQueue(int capacity, bool isMaxHeap = true, IComparer<T> cmp = null)
{
Count = 0;
Capacity = Math.Max(16, capacity);
IsMaxHeap = isMaxHeap;
Buffer = new T[Capacity];
if (cmp != null) Cmp = cmp;
else Cmp = Comparer<T>.Default;
}
private void Resize()
{
Capacity <<= 1;
Array.Resize(ref Buffer, Capacity);
}
public void Enqueue(T value)
{
if (Count == Capacity) Resize();
Buffer[Count] = value;
Count++;
UpHeap();
}
public T Dequeue()
{
var res = Buffer[0];
Swap(0, Count - 1);
Count--;
DownHeap();
return res;
}
public T Peek() { return Buffer[0]; }
private void Swap(int i, int j)
{
var tmp = Buffer[i];
Buffer[i] = Buffer[j];
Buffer[j] = tmp;
}
private void UpHeap()
{
var n = this.Count - 1;
while (n != 0)
{
var parent = (n - 1) / 2;
if (Compare(Buffer[n], Buffer[parent]) > 0)
{
Swap(n, parent);
n = parent;
}
else break;
}
}
private void DownHeap()
{
var parent = 0;
while (true)
{
var child = 2 * parent + 1;
if (child > this.Count - 1) break;
if (child < Count - 1 && Compare(Buffer[child], Buffer[child + 1]) < 0)
{
child += 1;
}
if (Compare(Buffer[parent], Buffer[child]) < 0)
{
Swap(parent, child);
parent = child;
}
else break;
}
}
private int Compare(T x, T y)
{
var res = Cmp.Compare(x, y);
if (!IsMaxHeap) res *= -1;
return res;
}
}
}C#だとどうしても優先度付きキューから実装しないとなので、コードを載せるとどうしても長くなります。
以上。
![[C#] ABC035 D トレジャーハントを解く](https://webbibouroku.com/wp-content/uploads/eye_atcoder.png)




コメントを書く